Question

Помогите решить.

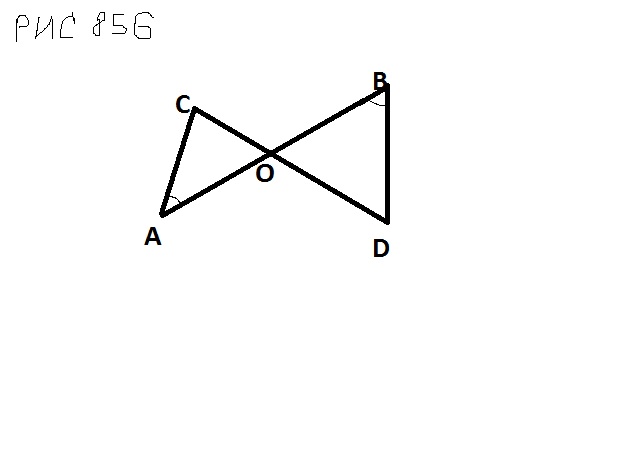
1. рис 856 (рис во вложении)

Обозначения знаков которые я использовал

"<" - угол

Дано:

<A=<B, CO=4, DO=6, AO=5

Найти а) OB 6) AC : BD в) Площадь AOC : площадь BOD

2. В треугольнике ABC AB=4см, BC=7см, AC=6см, а в треугольнике MNK MK = 8см, MN=12см, KN=14см. Найдите углы треугольника MNK, если <A=80 градусов, <B=60 градусов.

Answer 1

Итак, что мы имеем:

 

1

треугольник ABC подобен треугольнику MKN в соотношении 1:2 , т.е. MNAC=NKBC=ABMK=2 , => <C=<N , <A=<M , <B=<K .

Изравенства следует, что <M=80* , <K=60*

Т.к. сумма всех углов треугольника равна 180* , то <N=180*-60*-80*=40* ...

   Ответ: 40*.

 

2

треугольники подобны по 2 признаку подобия(<A=<B , <COA=<BOD - это вертекальные углы) , => CODO=AOBO=CABD

все стороны треугольника COA подобны сторонам треугольника BOD в отношении 2 к 3

т.к. CODO=46=23 (CO=2 , DO=6 - по условию)

Значит AC:BD=23

OCDO=AOOB

46=5OB

4OB=30

OB=7,5 (семь целых пять десятых)

Теперь найдём площадь:

P=(CO+AO+AC)2    (периметр)

S=корень из (P(P-CO)*(P-AO)*(P-CA))

 

Но к этой задаче эта формула не подходит, значит:

S1=12*CO*AO*sinCOA

S2=12*BO*DO*sinBOD

   

   S1S2=(CO*AO)(BO*DO)=2445

   S1S2=2445