Question

стороны трапеции равны 4 см 6 см 6см 10см .чему равна ее средняя линия

Answer 1

Сначала рассмотрим вариант равнобедренной трапеции с боковыми сторонами 6 и 6, и основаниями 10 и 4.
Отсюда средняя линия равна:

$l= frac{a+b}{2}= frac{10+4}{2}= frac{14}{2}=7 cm$

Теперь рассмотрим вариант существования трапеции с основаниями 10 и 6, и боковыми сторонами 4 и 6, и выявим её внешний вид:
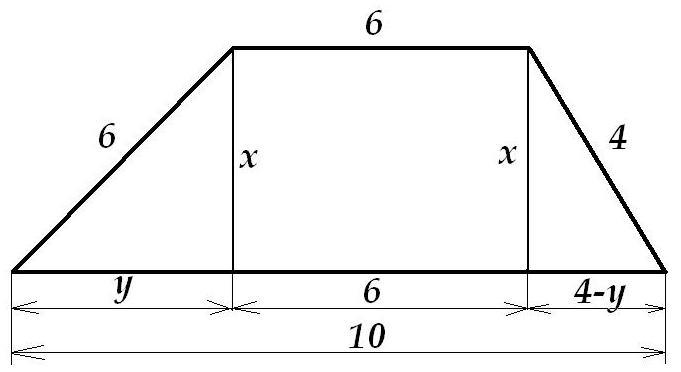
Расписывать долго не буду, смотрим рисунок:
Пусть на рисунке трапеция с основаниями 10 и 6, и боковыми сторонами 4 и 6. Все обозначения на рисунке, поехали:

$left { {{x^2+y^2=36} atop {x^2+(4-y)^2=16}} right.$

Выразим из обоих уравнений $X^2$ и приравняем полученные выражения между собой:

$left { {{x^2=36-y^2} atop {x^2=16-(4-y)^2}}right.\\36-y^2=16-(4-y)^2$

$36-y^2=16-16+8y-y^2\\8y=36\\y=4,5$

$4-y=4-4,5=-0,5$ - один из катетов меньшего треугольника, значит трапециия с параллельными сторонами 10 и 6, и двумя другими 6 и 4 будет иметь примерно такой вид, как на втором рисунке, что называется тупоугольной трапецией.

Средняя линия такой трапеции равна:

$l=frac{10+6}{2}=8 cm$

Answer 2

Во-первых, трапеция однозначно не прямоугольная. Во-вторых, такая трапеция строится" на ура". И не нужно говорить "сумничать". Некрасиво вам такое говорить по статусу.

Answer 3

Итак, "доказательства" как нет, так и нет.....

Answer 4

Согласен, приношу извинения! )) В заблуждение ввводит, то, что мы привыкли к "стандартному" виду трапеции, у которой оба угла при основании - острые; но забываем при этом о существовании тупоугольной трапеции. Ну и спасибо, за то, что пришлось повторить материал ))

Answer 5

так, а теперь нужно попросить модера, чтобы почистил переписку- она здесь не нужна. Я сейчас поправлю свое решение( уберу комменты) а вы добавьте в своем.

Answer 6

ОК

Answer 7

Существует 2 трапеции - с основаниями 4 и 10  и 6 и 10.
Соответственно и решений 2
1) (4+10)/2=7
2) )(6+10)/2=8

Answer 8

Смею заверить, что трапеции в варианте 2) не существует )))

Answer 9

Решение правильное, прошу снять нарушение!