Question

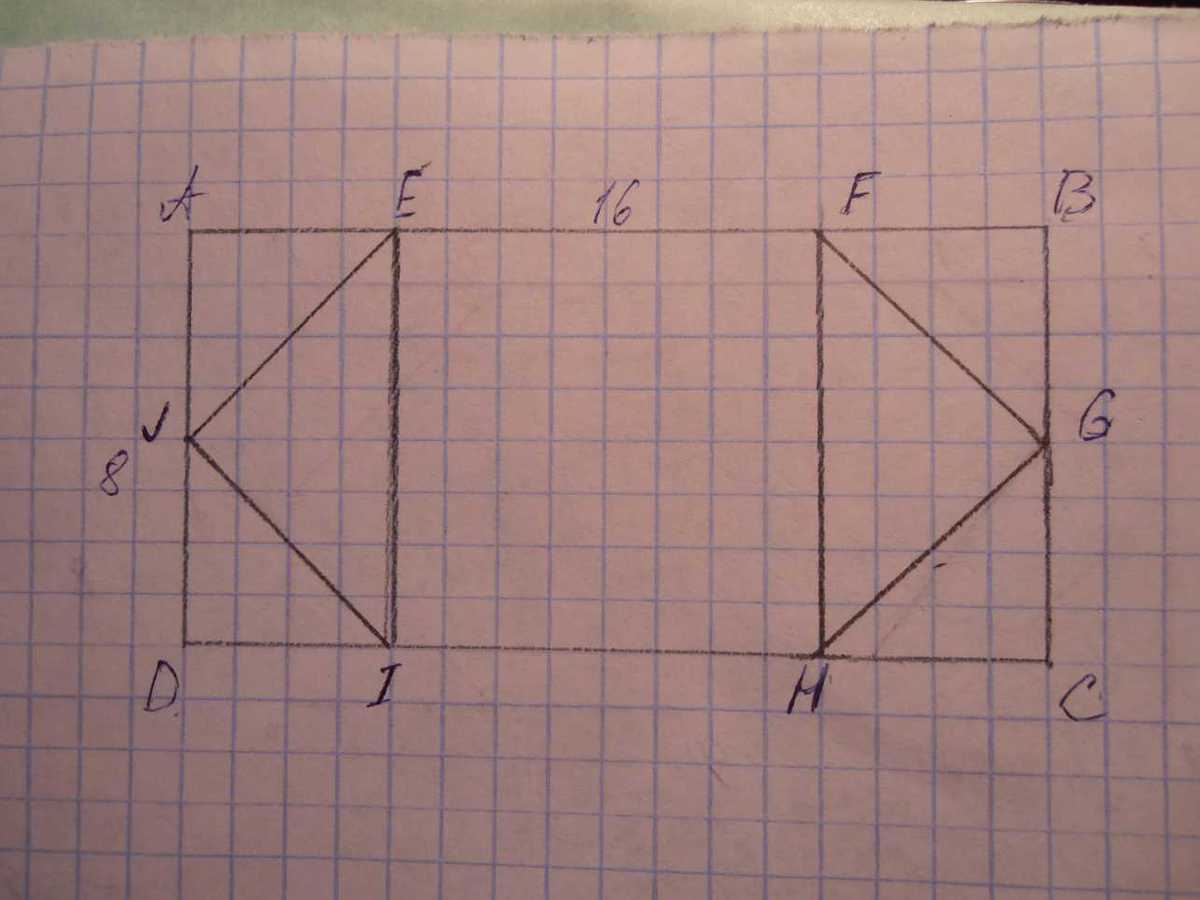
Прямоугольник со старинами 8 и 16 см. От его углов отрезали равные равнобедренные треугольники. Чему равна площадь получившегося шестиугольника.

Answer 1

По условию задачи
AB = CD = 16
BC = AD = 8
Решение:
AJ=AD/2
AE=AJ (т.к. треугольник равнобедренный)
JE=$sqrt{ AE^{2} + AJ^{2} }$ (по теореме Пифагора)
Площадь шестиугольника ровняется сумме площадей простых фигу на которые его можно разбить.
Разбиваем шестиугольник на простые фигуры:
треугольник с вершинами J E I
вычисляем площадь J E I по формуле Герона
квадрат с вершинами E F H I
вычисляем площадь квадрата E F H I (сторона EI=AD=6, площадь равна $EI^{2}$  
Площадь шестиугольника равна S(квадрата E F H I) + 2*S(треугольника J E I)