Предмет: Математика,
автор: nast09082001
Сколько существует целых чисел, удовлетворяющих неравенству:
|3x+7|< или = 2
Ответы
Автор ответа:
0
|3x+7|-2 0
0
Раскрываем модуль методом интервалов:
1. x
3x+7-2 0
0
3x+5 0
0
x
2. x<
-3x-7-2<0
-3x-9<0
3x>-9
x>-3
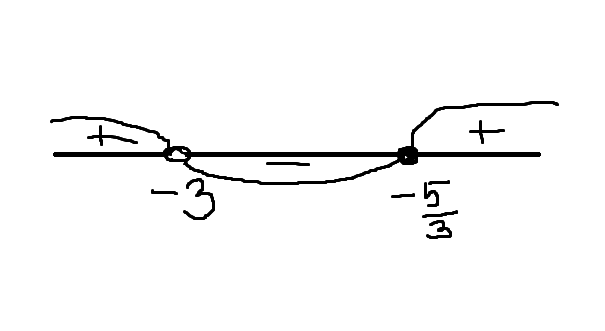
Строим числовую прямую (см. рисунок)
Точка -3 - выколотая, т.к. неравенство строгое. В интервале между -3 и -5/3 (примерно -1,66) есть только одно целое решение: -2.
Ответ: одно целое число удовлетворяет неравенству, это число -2.
Раскрываем модуль методом интервалов:
1. x
3x+7-2
3x+5
x
2. x<
-3x-7-2<0
-3x-9<0
3x>-9
x>-3
Строим числовую прямую (см. рисунок)
Точка -3 - выколотая, т.к. неравенство строгое. В интервале между -3 и -5/3 (примерно -1,66) есть только одно целое решение: -2.
Ответ: одно целое число удовлетворяет неравенству, это число -2.
Приложения:
Автор ответа:
0
В) (-1/4 ; + 8 плюс бесконечность)
Автор ответа:
0
У вас вопрос "сколько", а не какой промежуток. Да тут и близко нет никакой 1/4. Уверенны, что это вообще те ответы?
Автор ответа:
0
извините я перепутала вопросы
Автор ответа:
0
там есть ответы 1,4,2,6
Автор ответа:
0
Ответ 1
Похожие вопросы
Предмет: Русский язык,
автор: dayanaaas
Предмет: Биология,
автор: minecraft1234455
Предмет: Математика,
автор: abasov07
Предмет: Математика,
автор: haykik
Предмет: Математика,
автор: pogorelyy85