Question

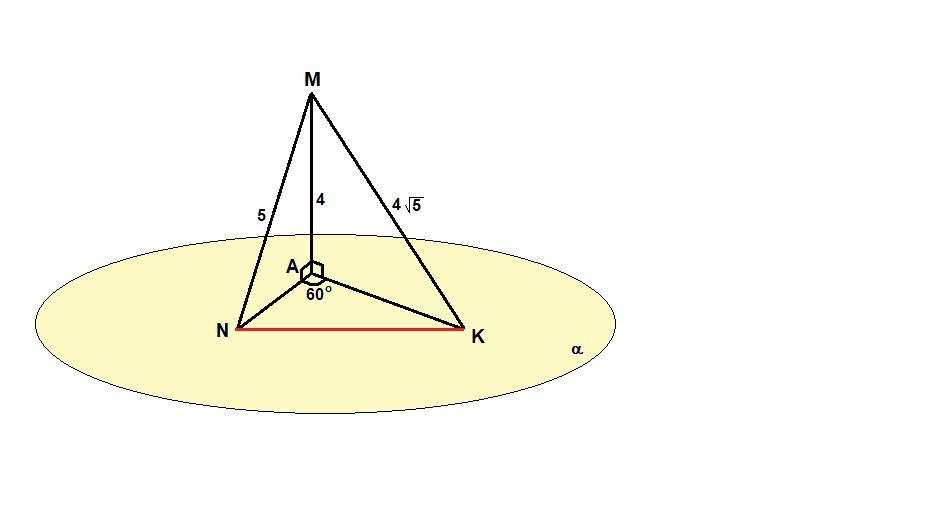
Із точки М до площини а(альфа) проведено перпендикуляр МА та похилі MN i MK.Кут між проекціями цих похилих дорівнює 60 градусів. Знайти NK, якщо МА=4см, MN=5 см, MK=4 корені з 5 см.

Answer 1

NK находим по т. косинусов   a2= b2+ c2−2bc ·cos(A)

NK2 = NA2+AK2- 2 NK*AK* cos60* 

рассмотрим треугольник NМА- прямоугольній, по тПифагора  NА=корень( МN2− МА2) =3см

рассмотрим  МАК-прямоуг, АК=корень( МК2−МА2) =8см

NK2 = NA2+AK2- 2 NK*AK* cos60*     NK2 = 32+82- 2 3*8* 1/2   NK= 7 см

Answer 2

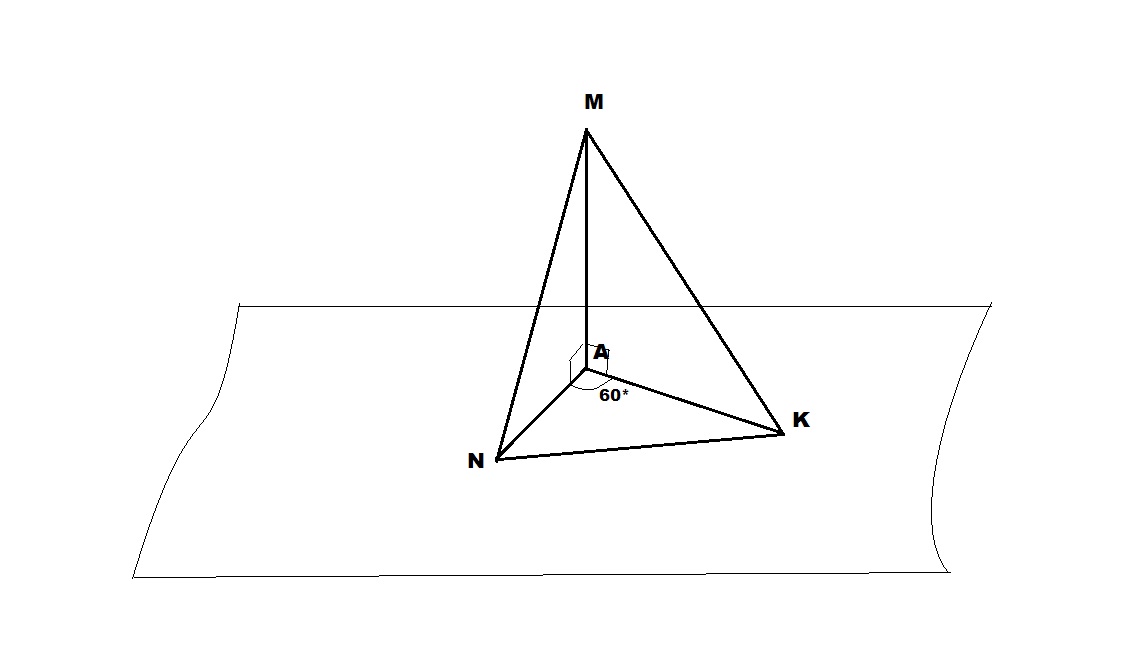
Ответ:

   7 см

Объяснение:

ΔMAN:

∠MAN = 90°, по теореме Пифагора:

NA = √(MN² - MA²) = √(25 - 16) = √9 = 3 см

ΔМАК:

∠МАК = 90°, по теореме Пифагора:

КА = √(МК² - МА²) = √(80 - 16) = √64 = 8 см

ΔNAK:

по теореме косинусов:

NK² = NA² + KA² - 2·NA·KA·cos∠NAK

NK² = 9 + 64 - 2 · 3 · 8 · 1/2

NK² = 73 - 24 = 49

NK = 7 см