Question

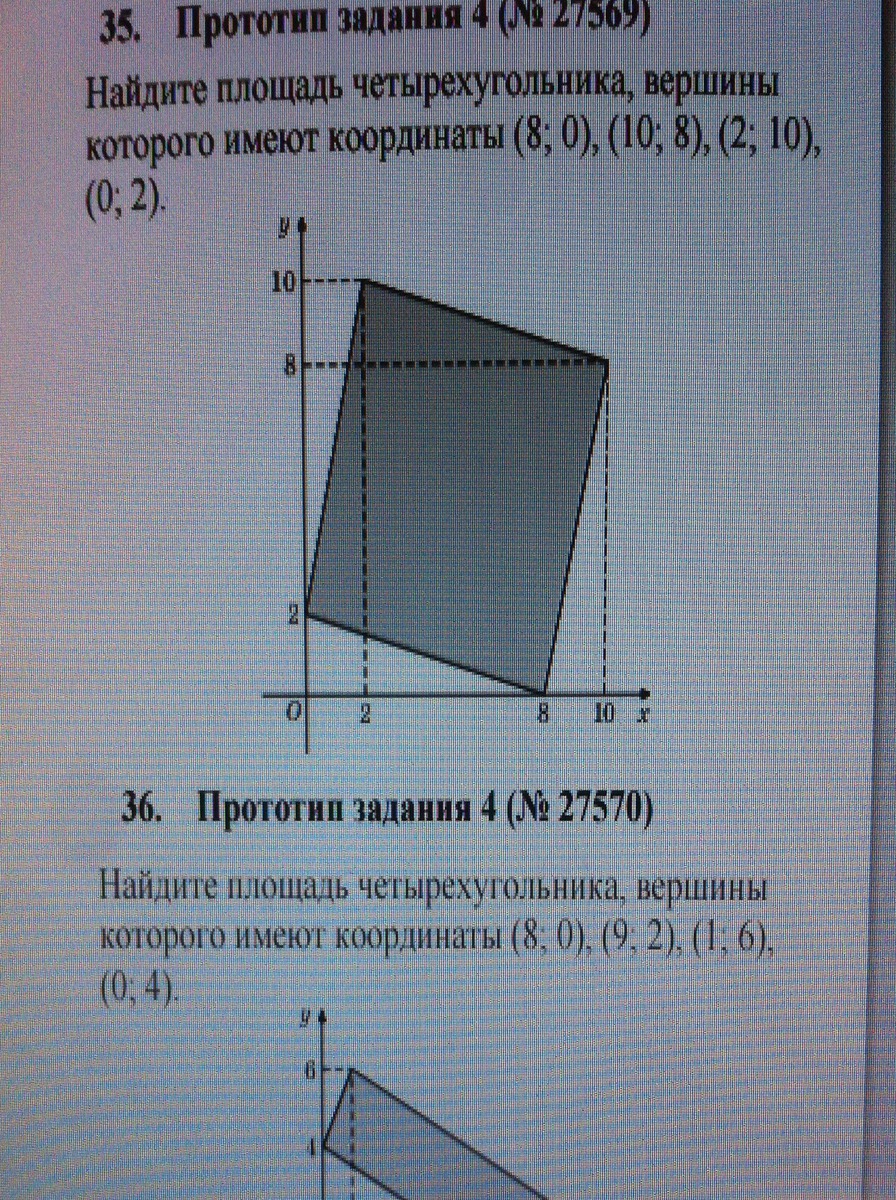
Найти площадь. 35 . Пожалуйста, напишите с решением)

Answer 1

Площадь прямоугольника равна двум площадям треугольников, где катеты - стороны. а гипотенуза - диагональ прямоугольника.
Площадь треугольника:
РАСЧЕТ ТРЕУГОЛЬНИКА ПО КООРДИНАТАМ:
Точка А                Точка В                   Точка С
Ха  Уа                    Хв  Ув                        Хс  Ус
8      0                     10    8                          2   10

Площадь треугольника S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 34
Площадь прямоугольника равна 2*34 = 68.

Можно найти длины сторон и по формуле Герона найти площадь:
1) Расчет длин сторон:
АВ = √((Хв-Ха)²+(Ув-Уа)²) = 8.246211251
BC = √((Хc-Хв)²+(Ус-Ув)²) = 8.246211251
AC = √((Хc-Хa)²+(Ус-Уa)²) = 11.66190379
       a                b               c                   p               2p            S
8.24621   11.6619    8.24621    14.07721   28.15432      34
cos A = 0.7071068 cos B = 0                    cos С = 0.707106781
Аrad = 0.7853982   Brad = 1.5707963    Сrad = 0.785398163
Аgr = 45                   Bgr = 90                      Сgr = 45
Получаем такой же результат S = 2*34 = 68.

Есть ещё третий вариант - выразить площадь через элементарные фигуры: сумма прямоугольника и трапеции и минус 3 площади треугольников.
S = 2*10+((10+8)/2)*8) -3*(1/2)*(2*8) =
    = 20 + 72 - 24 = 68.