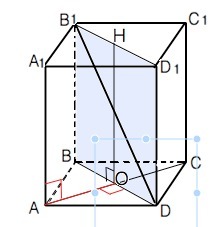
В правильной четырехугольной призме ABCDA1B1C1D1 площадь основания равна 16.Найти расстояние между прямыми АА1 и B1D. помогите решить пожалуйста!
Ответы
Прямые АА1 и В1D не пересекаются, не параллельны, лежат в разных плоскостях – они скрещивающиеся.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Расстоянием между прямой и плоскостью является длина отрезка, проведенного перпендикулярно к плоскости из любой точки прямой.
АА1║ВВ1⇒ АА1 параллельна плоскости, содержащей прямую В1D.
Т.к. призма правильная, АВСD – квадрат.
Диагонали квадрата взаимно перпендикулярны и точкой пересечения делятся пополам.
Проведем ОН║АА1. АО⊥ОН, АО⊥ВD⇒
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. ⇒
АО перпендикулярна плоскости, содержащей прямую B1D. Искомое расстояние АО.
S=АВ²⇒
AB=√16=4
Диагонали квадрата - биссектрисы прямых углов. ∠ОАВ=45°
АО=АВ•sin45°=4•√2/2=2√2 (ед. длины)