Question

ПОМОГИТЕ ПОЖАЛУЙСТА!!!

 

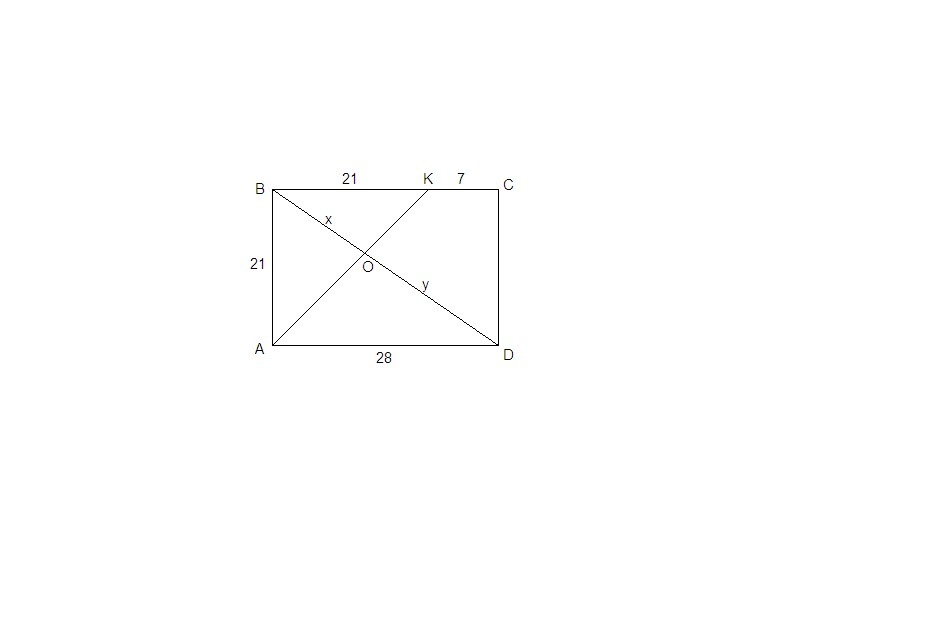
Биссектриса угла прямоугольника делит его сторону на отрезки 21 см и 7 см, считая от ближайшей к данному углу вершины. Найдите отрезки, на которые эта биссектриса делит диагональ прямоугольника.

Answer 1

∠ВАК = 90°/2 = 45°, значит ΔАВК прямоугольный равнобедренный,
АВ = ВК = 21 см

ВС = AD = 21 + 7 = 28 см

По теореме Пифагора из ΔABD:
BD = √(AB² + AD²) = √(441 + 784) = √1225 = 35 см

Биссектриса угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные прилежащим сторонам:
x : y = AB : AD
x : y = 21 : 28 = 3 : 4
4x = 3y

x + y = 35
y = 35 - x

4x = 3(35 - x)
4x = 105 - 3x
7x = 105
x = 15

BO = 15 см
OD = 35 - 15 = 20 см