Предмет: Математика,
автор: protsunxiusha
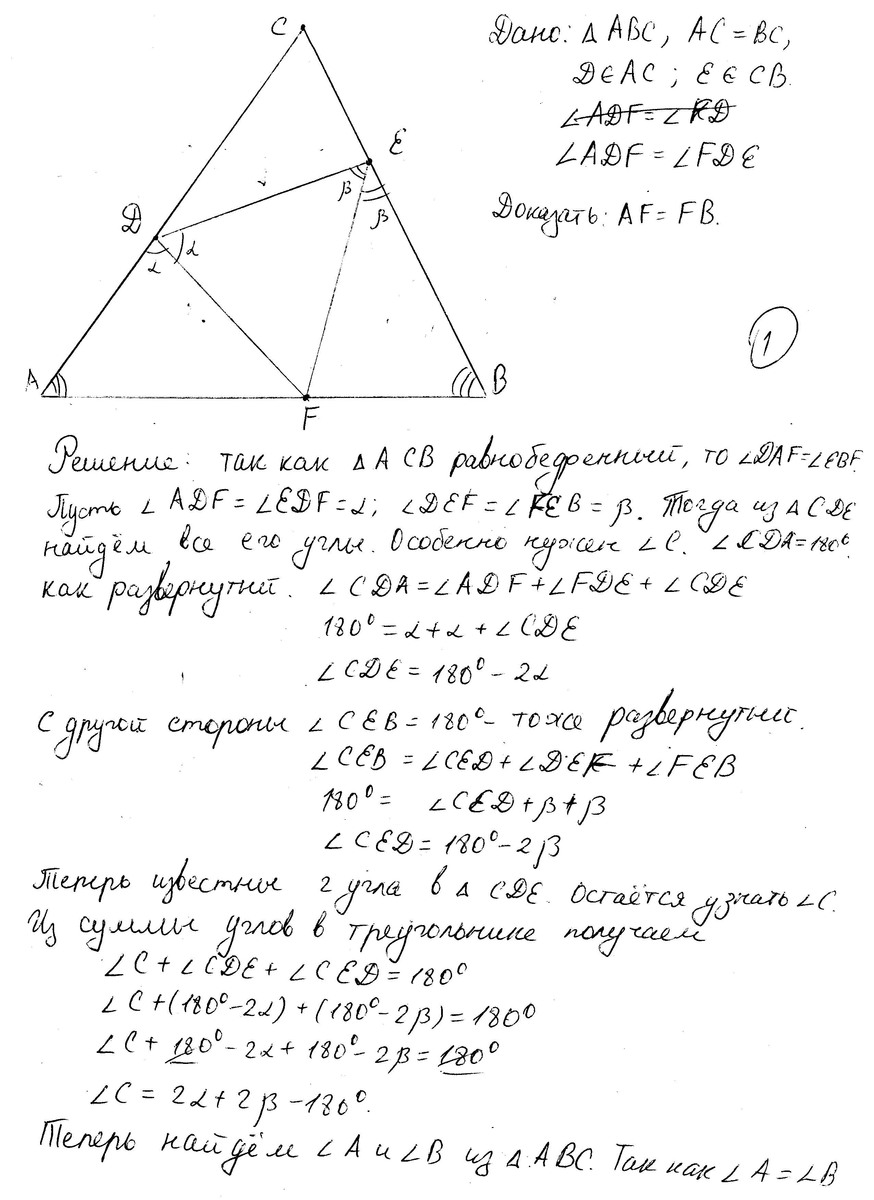
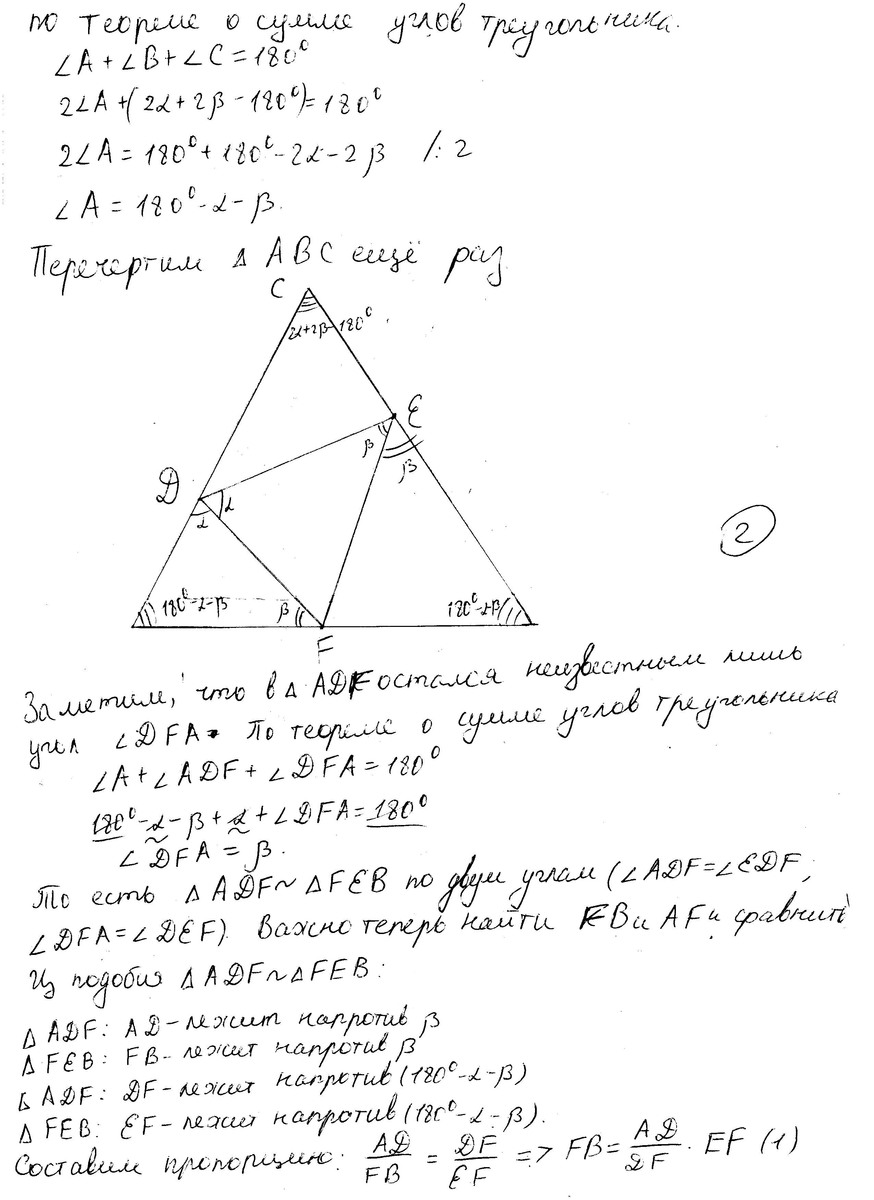
5. На боковых сторонах AC и BC равнобедренного треугольника ABC взяты точки D и E
соответственно. Точка F пересечения биссектрис углов DEB и ADE лежит на основании AB.
Докажите, что F — середина AB.
срочно!!!
Ответы
Автор ответа:
0
Доказательство заключается в следующем: исходя из того, что точка F принадлежит биссектрисе DEB, можно сделать вывод, что расстояние от точки F до прямых DE и BE одинаково. Соответственно и расстояния от F до AD и от F до DE одинаковы. И, если расстояния от F до прямых AD и BE одинаковы, то точка F лежит на биссектрисе угла ACB. Зная по условиям задачи, что треугольник ABC равнобедренный, откуда следует, что медиана и биссектриса совпадают, то тогда точка F лежит на медиане, и, следовательно, является серединой основания AB.
Автор ответа:
0
Решение в приложении. Очень длинное, но с чертежами.
Через подобие трех треугольников. Возможно есть более короткие решения.
Через подобие трех треугольников. Возможно есть более короткие решения.
Приложения:

Похожие вопросы
Предмет: История,
автор: nadinsob
Предмет: Английский язык,
автор: magagadjianko228
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: dfhjhf
Предмет: Математика,
автор: kakana