Предмет: Алгебра,
автор: BorDre
Вопрос по решению 4-ой и 5-ой системы
Приложения:
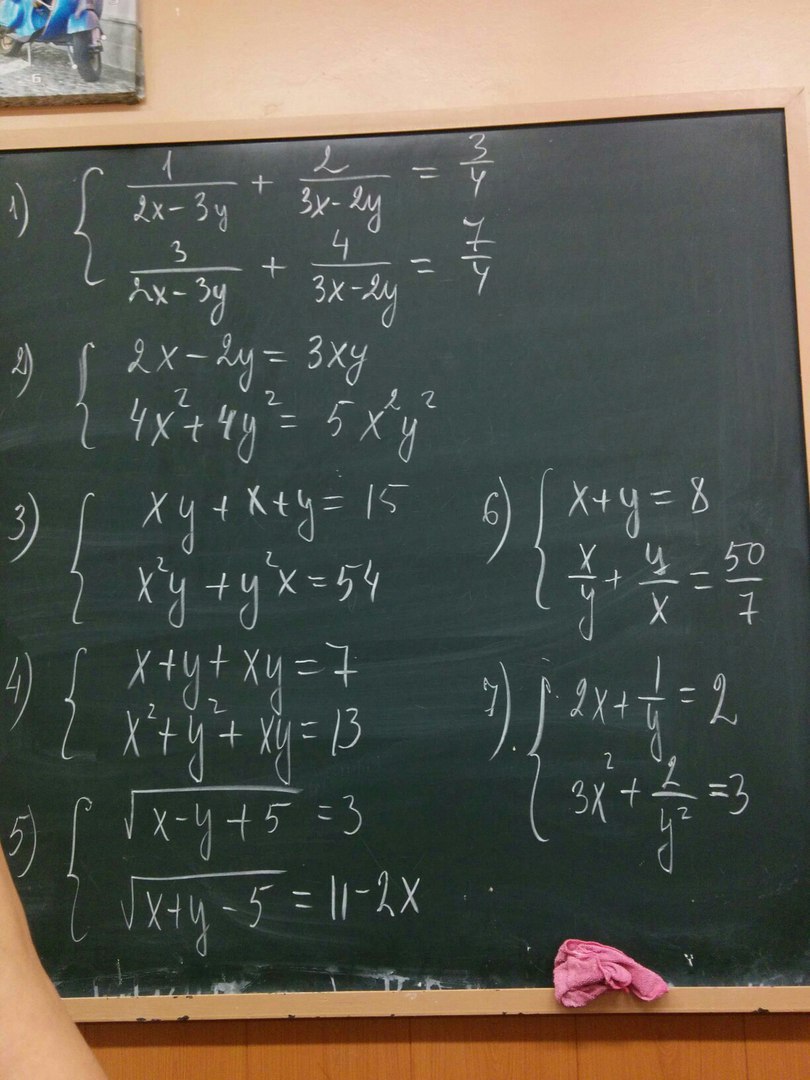
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: География,
автор: Filarewor
Предмет: Математика,
автор: izdat8872
Предмет: География,
автор: Galina55556
Предмет: Биология,
автор: 87i2qj8c
Предмет: Алгебра,
автор: artyrrik21