Предмет: Алгебра,
автор: IIIdenchikIII
под цыфрой 4 ,зарание спасибо)
Приложения:
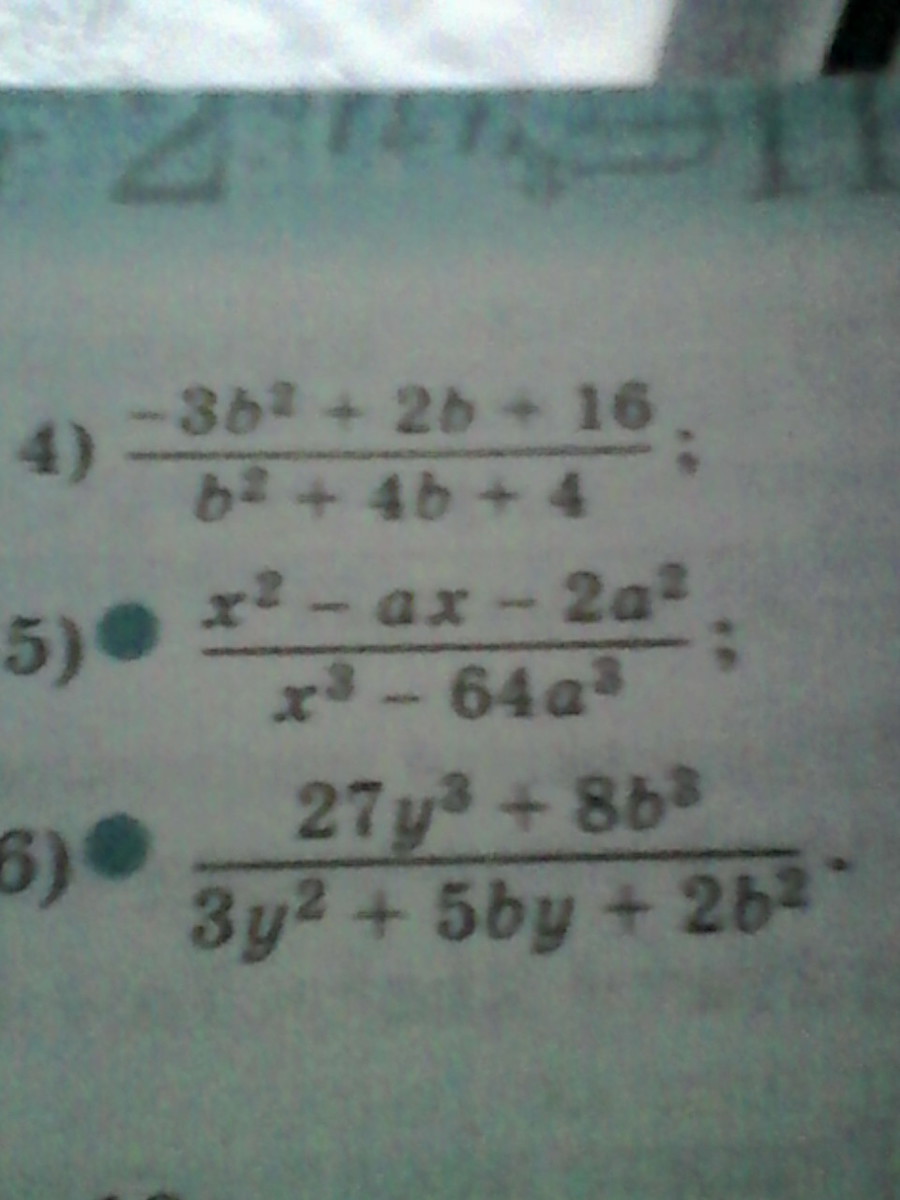
Ответы
Автор ответа:
0
Видим, что знаменатель дроби можно свернуть в формулу квадрата суммы
Чтобы дробь можно было сократить, разложим числитель на множители (то есть чтоб появились скобочки, как в числителе).
1) Для этого выпишем числитель и приравняем к нулю.
2) Найдём корни этого уравнения через дискриминант:
3) Корни нашли, теперь сворачиваем в скобочки(вынося коэффициент
4) Всё, мы это сделали! Получили скобки для числителя. И мы видим, что появляется одинаковое в числителе и знаменателе и можно сократить одинаковые скобки (множители):
Задача упростить выражение - решена!
Автор ответа:
0
спасибо , большое)
Похожие вопросы
Предмет: Алгебра,
автор: kolesnikviole
Предмет: Английский язык,
автор: ItIsMe1917
Предмет: Українська мова,
автор: sultanmaria74
Предмет: Геометрия,
автор: Igoroha007
Предмет: Алгебра,
автор: KENT56Rus