Предмет: Геометрия,
автор: Gfalka
Две точки, которые лежат на кругах разных основ цилиндра соединены отрезком. Найти его длину, если радиус равен 10 см, высота - 17 см, расстояние от оси к отрезку 4 см
Ответы
Автор ответа:
0
Две точки, которые лежат на кругах разных основ цилиндра соединены отрезком. Найти его длину, если радиус равен 10 см, высота - 17 см, расстояние от оси к отрезку 4 см
------
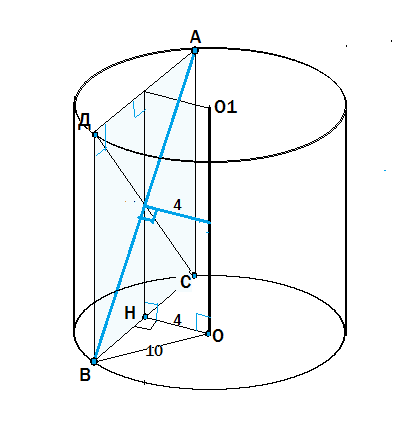
Уточним, что данные две точки, которые лежат на кругах разных основ цилиндра, расположены на окружностях, ограничивающих эти круги, а расстояние от оси к отрезку 4 см - это расстояние от оси цилиндра до отрезка 4 см.
Сделаем рисунок, назовем данный отрезок АВ.
АВ и ось цилиндра ОО1 - скрещивающиеся прямые, т.к. не параллельны и не пересекаются.
Расстояние между скрещиваюимися прямыми - это расстояние между одной из этих прямых и параллельной ей плоскостью, проходящей через другую прямую.
Проведем параллельно ОО1 плоскость, содержащую АВ. Для этого из А и В проведем к противоположным основаниям перпендикуляры АС и ВД.
Соединим все четыре точки. АС=ВД= высоте цилиндра =17 см
АДВС - прямоугольник, т.к. основания цилиндра параллельны и углы ДВС, АСВ=90º по построению..
АВ лежит в получившейся плоскости как диагональ этого прямоугольника.
Расстояние от прямой ОО1 до параллельной ей плоскости измеряют перпендикуляром.
Проведем из центра О перпендикуляр к хорде ВС.
ВН=НС по свойству радиуса и хорды.
Из прямоугольного треугольника ОНВ найдем длину НВ по т.Пифагора:
ВН²=ВО²-ОН²=100-16=84
ВН=√84
BC=2 BH=2√84
Из прямоугольного треугольника АВС по т. Пифагора найдем АВ:
АВ²=ВС²+АС²=4*84+289=625
АВ=√625=25 см
------
Уточним, что данные две точки, которые лежат на кругах разных основ цилиндра, расположены на окружностях, ограничивающих эти круги, а расстояние от оси к отрезку 4 см - это расстояние от оси цилиндра до отрезка 4 см.
Сделаем рисунок, назовем данный отрезок АВ.
АВ и ось цилиндра ОО1 - скрещивающиеся прямые, т.к. не параллельны и не пересекаются.
Расстояние между скрещиваюимися прямыми - это расстояние между одной из этих прямых и параллельной ей плоскостью, проходящей через другую прямую.
Проведем параллельно ОО1 плоскость, содержащую АВ. Для этого из А и В проведем к противоположным основаниям перпендикуляры АС и ВД.
Соединим все четыре точки. АС=ВД= высоте цилиндра =17 см
АДВС - прямоугольник, т.к. основания цилиндра параллельны и углы ДВС, АСВ=90º по построению..
АВ лежит в получившейся плоскости как диагональ этого прямоугольника.
Расстояние от прямой ОО1 до параллельной ей плоскости измеряют перпендикуляром.
Проведем из центра О перпендикуляр к хорде ВС.
ВН=НС по свойству радиуса и хорды.
Из прямоугольного треугольника ОНВ найдем длину НВ по т.Пифагора:
ВН²=ВО²-ОН²=100-16=84
ВН=√84
BC=2 BH=2√84
Из прямоугольного треугольника АВС по т. Пифагора найдем АВ:
АВ²=ВС²+АС²=4*84+289=625
АВ=√625=25 см
Приложения:
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: vera6332
Предмет: Физика,
автор: Аноним
Предмет: Химия,
автор: NichaKatya
Предмет: Химия,
автор: NichaKatya