Предмет: Алгебра,
автор: rus0209
Решите пожалуйста!
Во вложениях номер 241(4,5,6) ещё сверху 3 и 4 и 243 полностью
Приложения:
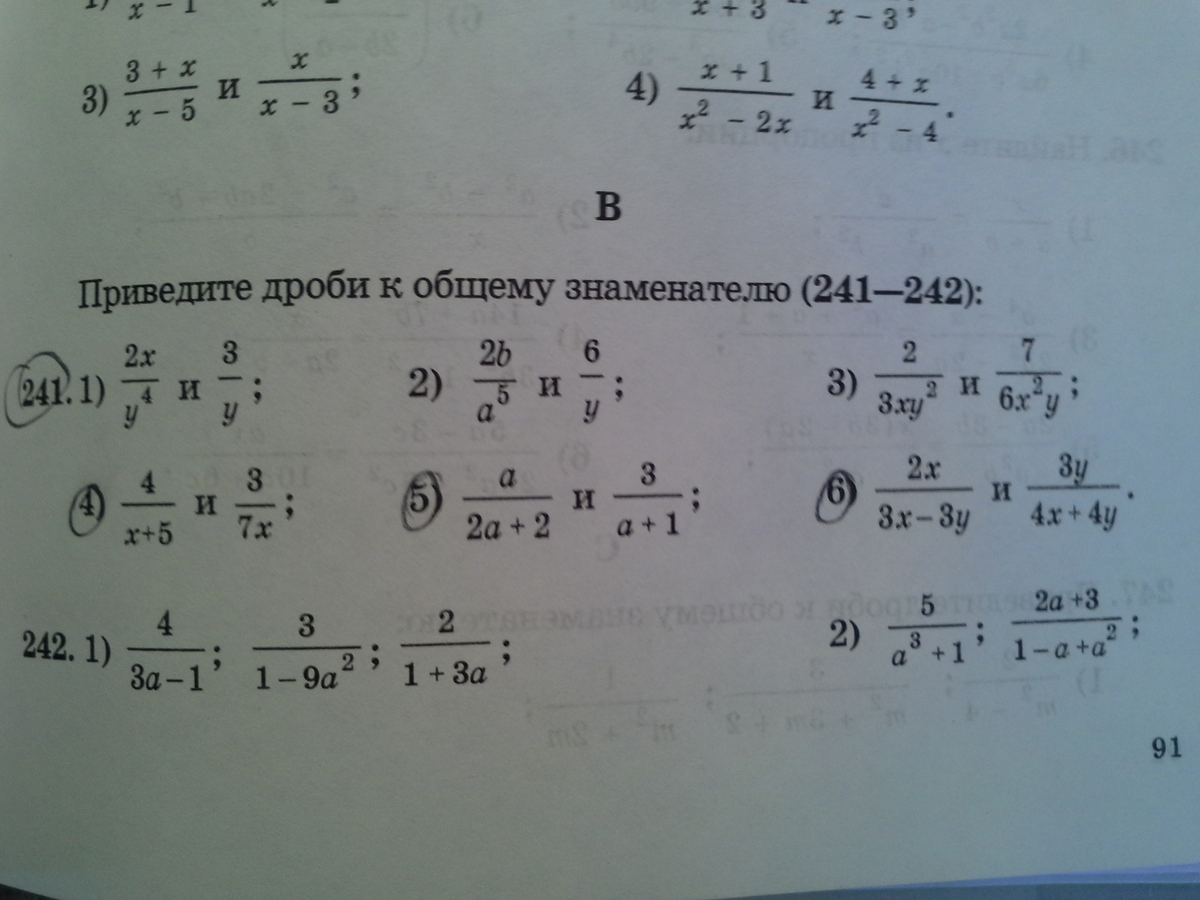
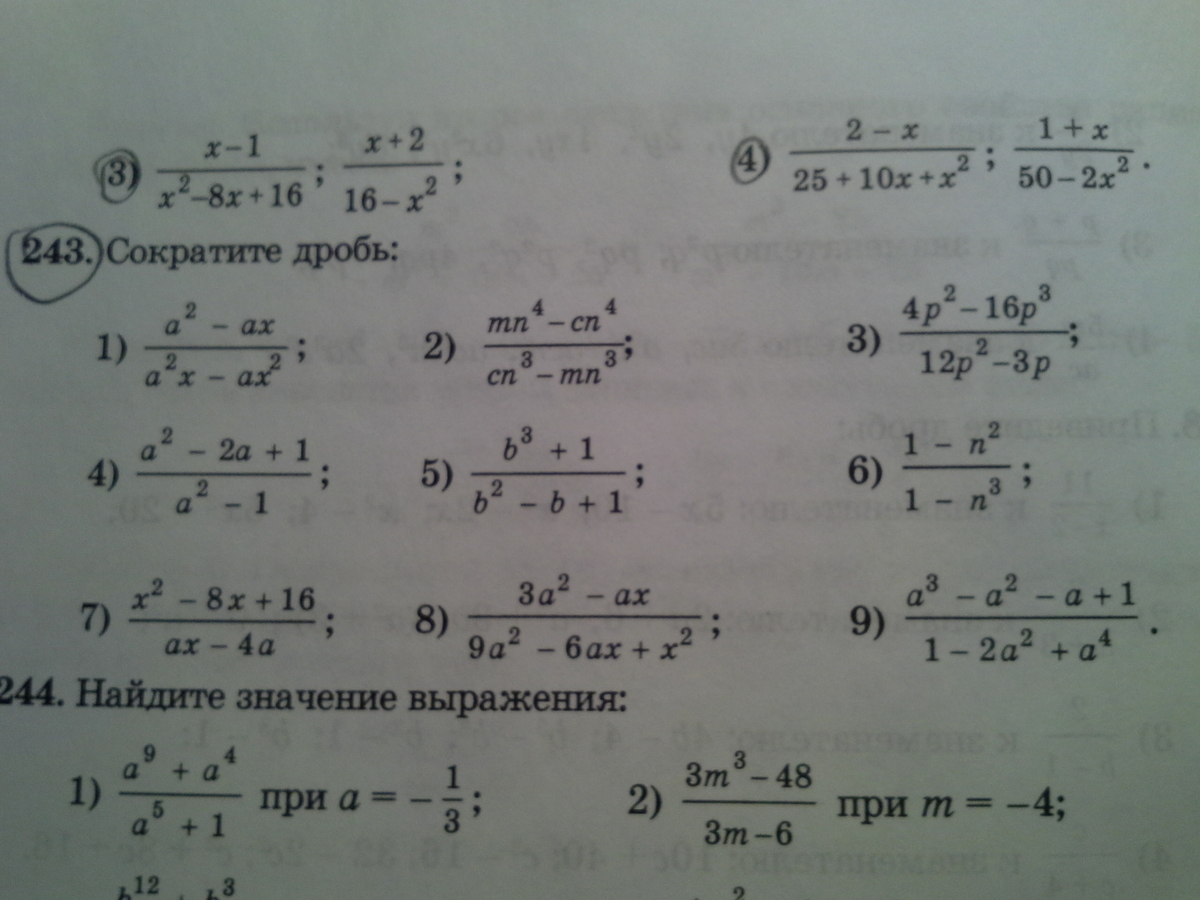
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: ppochemy
Предмет: Физика,
автор: sergg2
Предмет: Обществознание,
автор: annaionanova
Предмет: Математика,
автор: demoness228