Предмет: Алгебра,
автор: Stark1
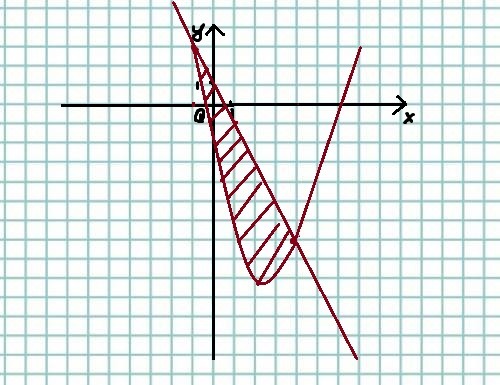
Найти площадь фигуры, ограниченной прямой y=1 - 2x и графиком функции y=x(в квадрате) - 5x - 3. Помогите пожалуйста решить.
Ответы
Автор ответа:
0
Найдем абсциссы точек пересечения прямой и параболы. Для этого решим систему уравнений.

Найдем определенный интеграл.

Ответ:
Найдем определенный интеграл.
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: alinaahmetbaj
Предмет: История,
автор: evalalala
Предмет: Алгебра,
автор: Анастасия201298
Предмет: Математика,
автор: кристис