Сделать подробно с чертежом с дано

Ответы
Диаметр круга радиусом 2 см совпадает с высотой, проведенной из вершины прямогоугла равнобедренного треугольника.Найдите площадь части круга, расположенной вне треугольника.
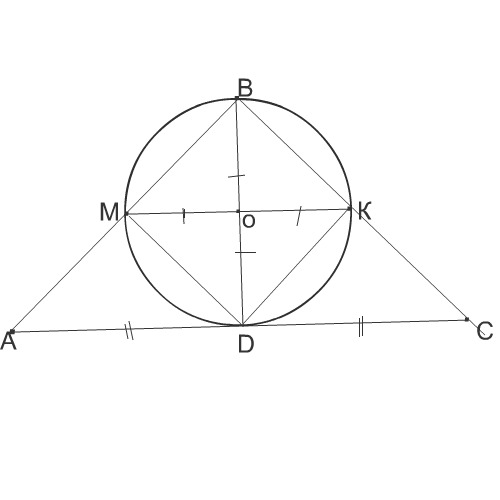
Сделаю свой рисунок.
Обозначим точки пересечения окружности с треугольником М, К,точку касания с основанием треугольника - D.
Соединим все эти точки.
Высота треугольника, как медиана прямоугольного треугольника, равна половине основания.
ВD=AD=DC
∆ АDВ= ∆ ВDС.
МК - диаметр окружности и средняя линия ∆ АВС,т.к. проходит через центр окружности.
МК=2 см
АМ=МВ, ВК=КС, МD=DK
МВКD - квадрат, диагонали которого равны диаметру окружности 2 см.
Площадь квадрата равна половине произведения его диагоналей.
S МВКD=2*2:2=2 см²
S окружности = πr²=4π
Площадь четырех сегментов круга вне квадрата МВКD равна
S окружности минус S МВКD =4π-2
Площадь сегментов вне треугольника равна половине площади четырех сегментов вне квадрата МВКD и равна:
(4π-2):2=(2π-1 )см²