Предмет: Математика,
автор: dvdya
Помогите решить три задания по тригонометрии:
Приложения:
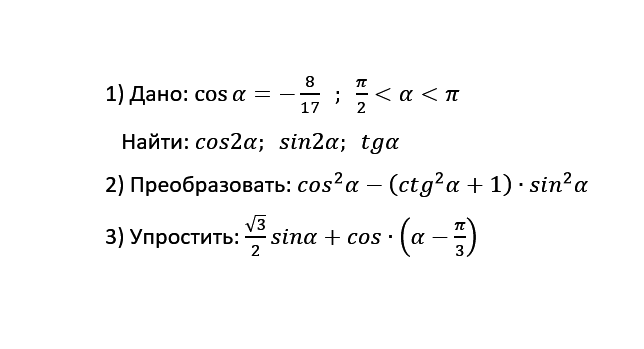
Ответы
Автор ответа:
0
1) Cos2α=2Cos²α - 1= 2(-8/17)² - 1= 2· 64/289 - 1= - 161/289
Sin2α = 2Sinα·Cosα=2·[-√(1 - Cos²α)] · Cosα= - 2√(1 - 64/289) · (- 8/17) =
= -2·15/17·(-8/17)= 240/289
Sin2α= +/- √(1 - Cos²2α) при x∈[π/2;π] Sinx>0 ⇒
Sin2α=√(1 - (-161/289)²) = 240/289
tgα = +/- √[(1-cos2α)/(1+cos2α)] при x∈[π/2;π] tgx<0 ⇒
tgα= - √[(1-(-161/289)/(1+(-161/289))] = - √[450/289 ·128/289]= - 240/289
2) Cos²α - Ctg²α·Sin²α - Sin²α = Cos²α - Cos²α - Sin²α = - Sin²α
3) √3/2·Sinα + Cosα·Cos(π/3) - Sinα ·Sin(π/3) = √3/2·Sinα +
+1/2·Cosα - √3/2·Sinα = 1/2·Cosα
Sin2α = 2Sinα·Cosα=2·[-√(1 - Cos²α)] · Cosα= - 2√(1 - 64/289) · (- 8/17) =
= -2·15/17·(-8/17)= 240/289
Sin2α= +/- √(1 - Cos²2α) при x∈[π/2;π] Sinx>0 ⇒
Sin2α=√(1 - (-161/289)²) = 240/289
tgα = +/- √[(1-cos2α)/(1+cos2α)] при x∈[π/2;π] tgx<0 ⇒
tgα= - √[(1-(-161/289)/(1+(-161/289))] = - √[450/289 ·128/289]= - 240/289
2) Cos²α - Ctg²α·Sin²α - Sin²α = Cos²α - Cos²α - Sin²α = - Sin²α
3) √3/2·Sinα + Cosα·Cos(π/3) - Sinα ·Sin(π/3) = √3/2·Sinα +
+1/2·Cosα - √3/2·Sinα = 1/2·Cosα
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: myname009
Предмет: Алгебра,
автор: lsafronova88
Предмет: Математика,
автор: ana0000
Предмет: Математика,
автор: Flower1611