Предмет: Геометрия,
автор: Мартышка7
Решите задачу. Конус
Приложения:
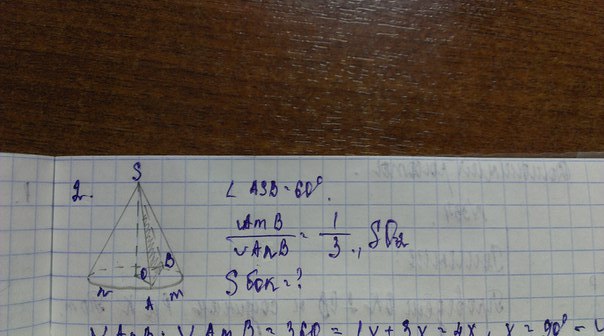
Ответы
Автор ответа:
0
S(бок) =πRL , где R -радиус основания , L - образующий .
ΔASB - равносторонний .
(один из углов равнобедренного треугольника =60° : AS =BS , ∠ASB =60°) .
L =AS=BS =AB.
дугаAmB =x , дуга AnB = 3x ⇒x+3x =360°(дугаAmB + дуга AnB =360°)⇔x=90°.
∠AOB =дугаAmB =90°.
Из Δ AOB по теореме Пифагора : AB =√(R² +R²) =R√2.
Следовательно: S(бок) =πR*R√2=πR²√2 .
Из Δ AOS тоже по теореме Пифагора : AS² - AO² = SO² ⇔AB² -AO²=SO² ;
(R√2)² -R² =SO² ⇒R² =SO² =4.
----
S(бок) =πR²√2 =π2²√2 =4√2π.
ответ : 4√2π.
ΔASB - равносторонний .
(один из углов равнобедренного треугольника =60° : AS =BS , ∠ASB =60°) .
L =AS=BS =AB.
дугаAmB =x , дуга AnB = 3x ⇒x+3x =360°(дугаAmB + дуга AnB =360°)⇔x=90°.
∠AOB =дугаAmB =90°.
Из Δ AOB по теореме Пифагора : AB =√(R² +R²) =R√2.
Следовательно: S(бок) =πR*R√2=πR²√2 .
Из Δ AOS тоже по теореме Пифагора : AS² - AO² = SO² ⇔AB² -AO²=SO² ;
(R√2)² -R² =SO² ⇒R² =SO² =4.
----
S(бок) =πR²√2 =π2²√2 =4√2π.
ответ : 4√2π.
Автор ответа:
0
Можно было без предусловия. Звучит слишком высокомерно... Зачем дальнее плавание ,если решается очень просто. Другое дело в конце (когда получилось , что в прямоугольном ΔAOS гипотенуза AS =R√2,один катет OA=R⇒другой SO тоже будет =R) проводить исследование и применить другой подход. А сознательное дополнительное построение никто не может отвергать.
Автор ответа:
0
Слишком "высокомерно"? Сейчас будет еще более слишком. Сама задача тривиальная, она в уме решается за 10 секунд. Тут вообще не о чем говорить. Но есть вещи ИНТЕРЕСНЫЕ и СКУЧНЫЕ. Вот я показываю, что ИНТЕРЕСНО, но это - оказывается - для вас "слишком высокомерно" и "дальнее плавание", которое "зачем".
Автор ответа:
0
Я повторю, "зачем". Я достроил пирамиду AOBS до октаэдра. Понятно, как расположены вершины? Три на окружности, и еще одна - симметрично S относительно плоскости основания конуса. То есть ВСЕ, что я сделал - отметил 4 точки - три на окружности и одну на продолжении SO за точку O, и сказал - это вершины октаэдра. А сечение этого октаэдра плоскостью AOS - квадрат. Так же, как плоскостью AOB или плоскостью BOS. Что означает SO = AO = OB. Заметьте, мое "дальнее плавание" уже закончилось.
Автор ответа:
0
Кстати, на окружности даже не три, а только две :)))
Автор ответа:
0
Блин, так можно всех запутать :) Пусть точка C - на окружности, AC - диаметр (то есть проходит через O) и BD - тоже диаметр. Пусть S1 лежит на SO, так что S1O = SO. Тогда (вот оно - решение :) ) SABCDS1 - октаэдр (потому что все его грани - правильные треугольники). Далее, у октаэдра все три сечения, перпендикулярные большим диагоналям (AC, BD и SS1) - квадраты. А все вершины равноудалены от центра O. Почему это ИНТЕРЕСНО? Да потому, что включает "движок" в голове. :)))
Похожие вопросы
Предмет: История,
автор: albina8487
Предмет: Математика,
автор: zohrabovazejnab97
Предмет: География,
автор: tahidagaragimov
Предмет: Математика,
автор: sabrie
Предмет: Обществознание,
автор: Futbolist21veka