Question

Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь этого прямоугольника!

Answer 1

P=56

c=27

 

P=2a+2b

56=2a+2b

28=a+b

a=28-b

 

по т. Пифагора:

с²=a²+b²

27²=(28-b)²+b²

729=b²+784-56b+b²

2b²-56b+55=0

b1=14-√337/2

b2=14+√337/2

 

тогда

a1=28+14-√337/2=42-√337/2

a2=28+14+√337/2=42+√337/2

 

S=a*b

S1=(42-√337/2)*14-√337/2

S2=(42+√337/2)*(14+√337/2)

 

либо ошибка в условии с цифрами. либо я запуталась(((

 

Answer 2

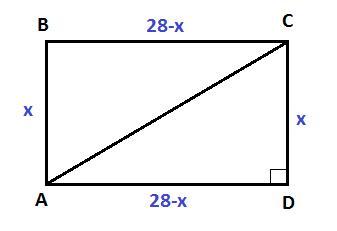
Дано : прямоугольник ABCD,  $P_{ABCD}=56;~AC=27$

Найти : $S_{ABCD}$

Решение :

$P_{ABCD}=2cdot(AD+CD)=56\~~~~~~~~~~~~~~~~~~~AD+CD=28~~Rightarrow~~~boldsymbol{AD=28-CD}$

ΔACD -  прямоугольный. Теорема Пифагора

$AD^2+CD^2=AC^2\(28-CD)^2+CD^2=27^2\28^2-2cdot 28CD+CD^2+CD^2=729\2CD^2-56CD+784-729=0\\2CD^2-56CD+55=0\\dfrac D4=bigg(dfrac b2bigg)^2-ac=bigg(dfrac {56}2bigg)^2-2cdot55=784-110=674\\CD=dfrac{-dfrac b2pmsqrt{dfrac D4}}a=dfrac{28pmsqrt{674}}2=14pmsqrt{168,5}$

$1)~CD=14+sqrt{168,5}\~~~~~AD=28-Big(14+sqrt{168,5}Big)=14-sqrt{168,5}\\2)~CD=14-sqrt{168,5}\~~~~~AD=28-Big(14-sqrt{168,5}Big)=14+sqrt{168,5}$

$S_{ABCD}=ADcdot CD=\\=Big(14-sqrt{168,5}Big)Big(14-sqrt{168,5}Big)=\\=14^2-sqrt{168,5}^2=196-168,5=27,5$

Ответ : 27,5