Question

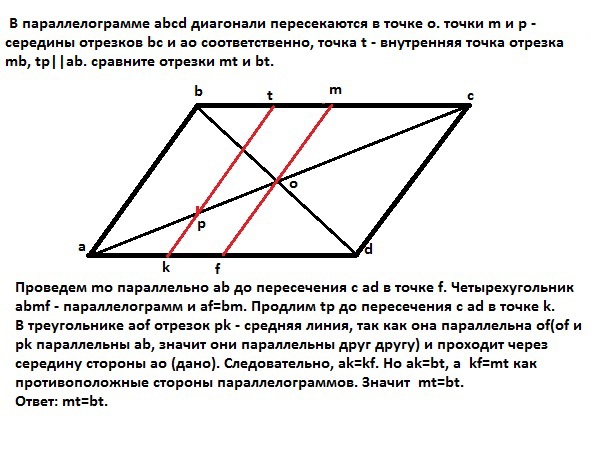
В параллелограмме abcd диагонали пересекаются в точке o. точки m и p - середины отрезков bc и ao соответственно, точка t - внутренняя точка отрезка mb, tp||ab. сравните отрезки mt и bt. ответ поясните

Answer 1

Проведем mо параллельно ab до пересечения с ad в точке f.
Четырехугольник abmf - параллелограмм и af=bm.
Продлим tp до пересечения с ad в точке k.
В треугольнике aof отрезок pk - средняя линия, так как она параллельна of (of и pk параллельны ab, значит они параллельны друг другу) и проходит через середину стороны ao (дано). Следовательно, ak=kf. Но ak=bt, a  kf=mt как противоположные стороны параллелограммов. Значит  mt=bt.
Ответ: mt=bt.