Предмет: Алгебра,
автор: Мартышка7
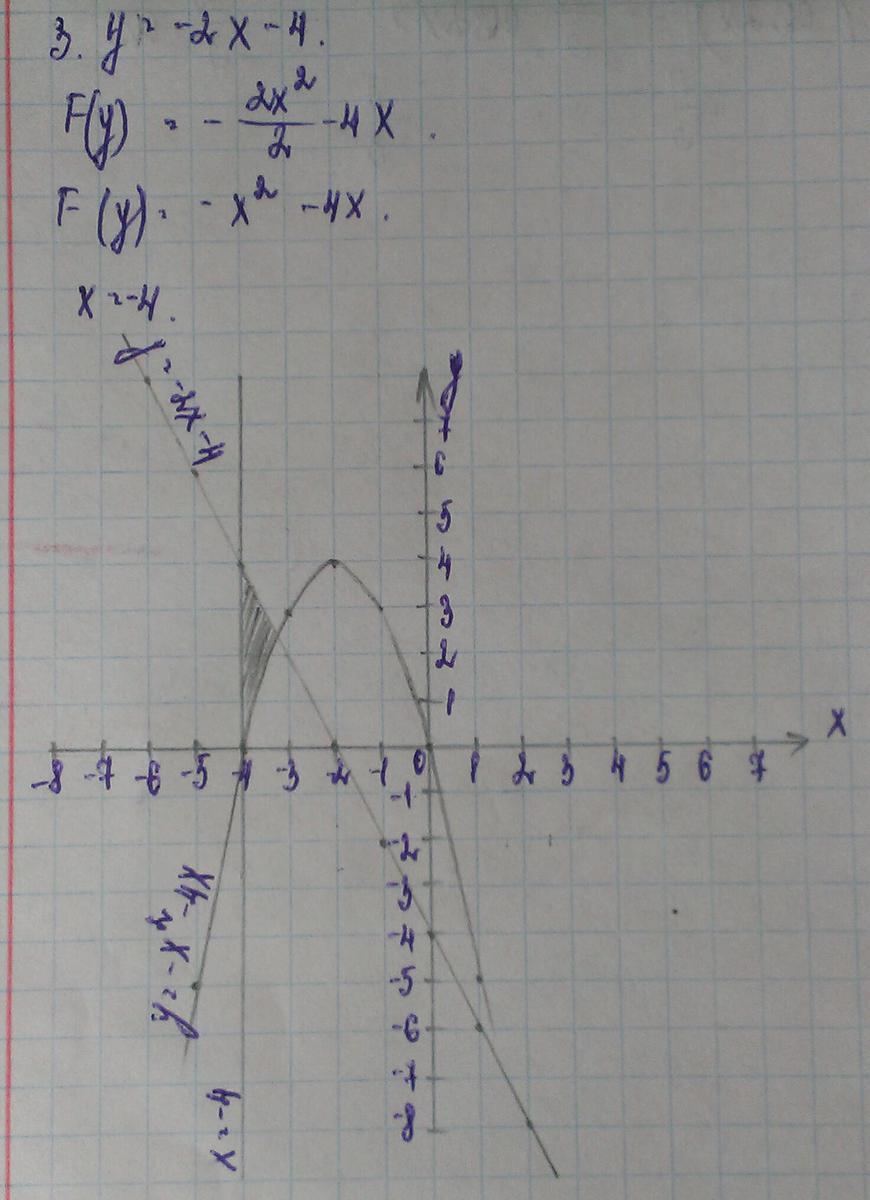
Найдите площадь фигуры, кот. ограничена линиями
Приложения:
Ответы
Автор ответа:
0
Точки пересечения:

Похожие вопросы
Предмет: Химия,
автор: melekakarina
Предмет: Информатика,
автор: Аноним
Предмет: Биология,
автор: Jalina123
Предмет: История,
автор: zhenyazx