Предмет: Геометрия,
автор: obey1mactep
Отрезок пересекает плоскость; а его концы отстоят от плоскости на 3 и 12 см. Найти расстояние от середины этого отрез
Ответы
Автор ответа:
0
Так как в условии ничего нет про угол, под которым отрезок пересекает плоскость, примем его за 90°. В этом случае действительно можно говорить о том, что расстояния от концов отрезка до плоскости являются частями самого отрезка, то есть перпендикуляры из концов отрезка на плоскость совпадают с самим отрезком.
Тогда длина отрезка: L = h₁+h₂ = 3 + 12 = 15 (cм)
и L/2 = 7,5 (cм)
Так как концы отрезка находятся по разные стороны плоскости, расстояние от середины отрезка до плоскости будет меньше половины длины отрезка на величину расстояния от ближнего к плоскости конца отрезка до самой плоскости. То есть:
h = L/2 - h₁ = 7,5 - 3 = 4,5 (см)
Ответ: расстояние от середины отрезка до плоскости 4,5 см
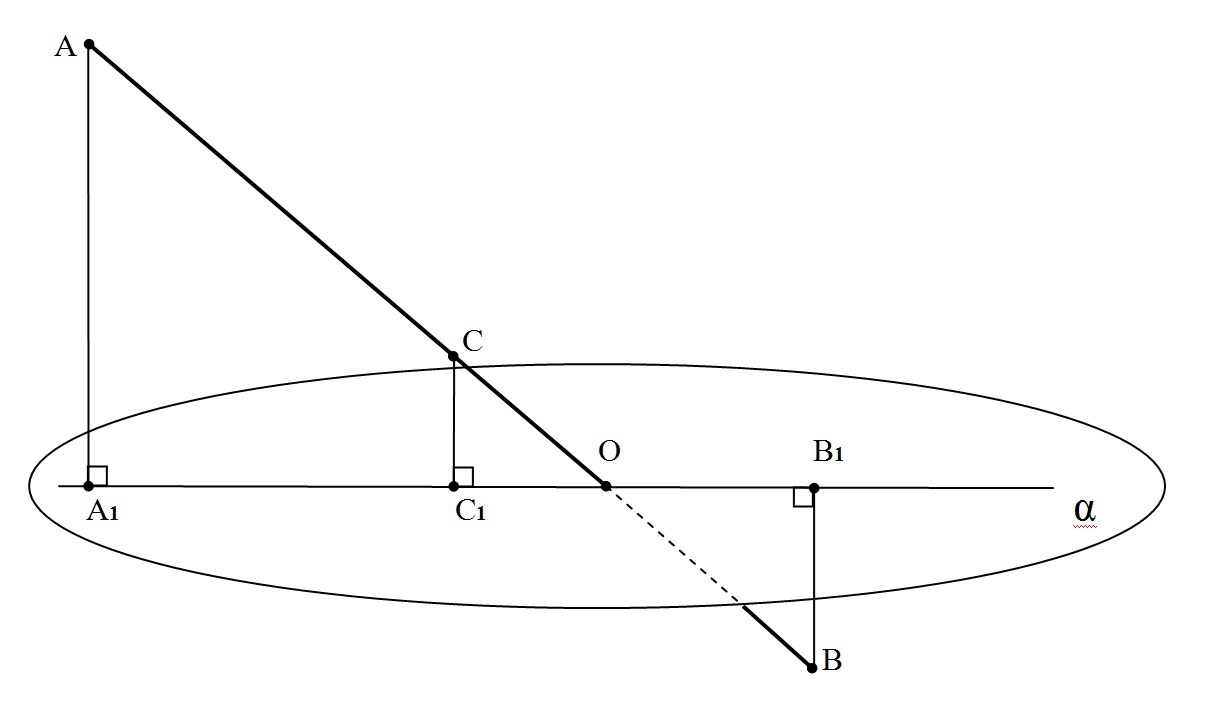
Решение через подобие треугольников. (см. рис.)
Расстоянием от точки до плоскости является перпендикуляр, опущенный из этой точки на данную плоскость.
Следовательно, АА₁⊥α и ВВ₁⊥α.
Через точки А₁ и В₁ проведем прямую А₁В₁.
Рассмотрим треугольники АА₁О и ВВ₁О:
Данные треугольники являются прямоугольными и
∠АОА₁=∠ВОВ₁, как вертикальные.
Значит, данные треугольники подобны по двум углам, и АО/ОВ = 12/3 = 4
Обозначим ОВ₁=х, тогда ОА₁=4х
Весь отрезок АВ=х+4х=5х, и половина отрезка АВ:2 = АС = СВ = 5х:2 = 2,5х
Тогда отрезок ОС = 4х-2,5х = 1,5х
Рассмотрим треугольники АОА₁ и СОС₁:
Так как СС₁⊥α => CC₁⊥A₁B₁
∠АОА₁ - общий
Следовательно, эти треугольники также подобны по двум углам, и
АО/CO = 12/CC₁
4x/1,5x = 12/CC₁
CC₁ = 12*1,5/4 = 4,5 (см)
Ответ: 4,5 см
Тогда длина отрезка: L = h₁+h₂ = 3 + 12 = 15 (cм)
и L/2 = 7,5 (cм)
Так как концы отрезка находятся по разные стороны плоскости, расстояние от середины отрезка до плоскости будет меньше половины длины отрезка на величину расстояния от ближнего к плоскости конца отрезка до самой плоскости. То есть:
h = L/2 - h₁ = 7,5 - 3 = 4,5 (см)
Ответ: расстояние от середины отрезка до плоскости 4,5 см
Решение через подобие треугольников. (см. рис.)
Расстоянием от точки до плоскости является перпендикуляр, опущенный из этой точки на данную плоскость.
Следовательно, АА₁⊥α и ВВ₁⊥α.
Через точки А₁ и В₁ проведем прямую А₁В₁.
Рассмотрим треугольники АА₁О и ВВ₁О:
Данные треугольники являются прямоугольными и
∠АОА₁=∠ВОВ₁, как вертикальные.
Значит, данные треугольники подобны по двум углам, и АО/ОВ = 12/3 = 4
Обозначим ОВ₁=х, тогда ОА₁=4х
Весь отрезок АВ=х+4х=5х, и половина отрезка АВ:2 = АС = СВ = 5х:2 = 2,5х
Тогда отрезок ОС = 4х-2,5х = 1,5х
Рассмотрим треугольники АОА₁ и СОС₁:
Так как СС₁⊥α => CC₁⊥A₁B₁
∠АОА₁ - общий
Следовательно, эти треугольники также подобны по двум углам, и
АО/CO = 12/CC₁
4x/1,5x = 12/CC₁
CC₁ = 12*1,5/4 = 4,5 (см)
Ответ: 4,5 см
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: marinkaberezka60
Предмет: Математика,
автор: urazbaevaaima87
Предмет: История,
автор: daniaradema41
Предмет: Математика,
автор: hhh999
Предмет: Химия,
автор: НастюшкаЛ