Предмет: Алгебра,
автор: mocor
Неравенство, нужно достаточно подробное решение.
Приложения:
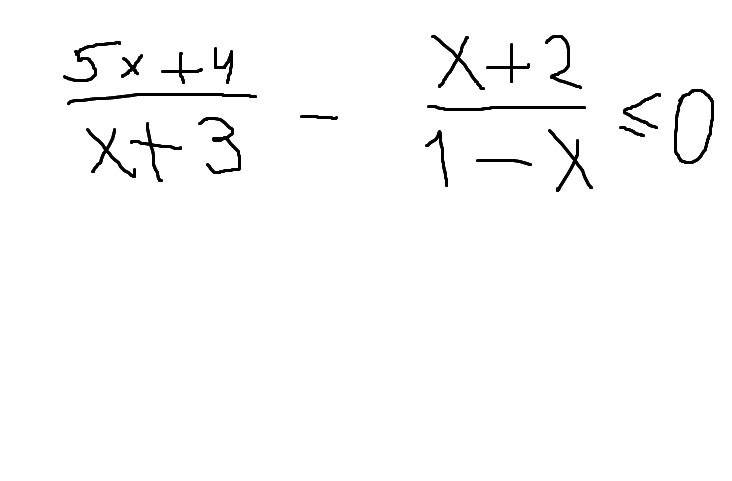
Ответы
Автор ответа:
0
а=3>0 и D>0, cледовательно, числитель дроби больше нуля при любом значении переменной х.
+ - +
_______________-3\\\\\\\\\\\\\\\\\\\\1________________
х∈(-3;1)
Автор ответа:
0
Благодарю!
Похожие вопросы
Предмет: Геометрия,
автор: 30novikova30
Предмет: Биология,
автор: fasteer
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: angelina2biste