Предмет: Геометрия,
автор: 2gaiver
отрезки АВ и СД имеют общую середину О .доказать треугольник АОС=ВОД
Ответы
Автор ответа:
0
т.к. О - середина , то
АО=ОВ
СО=ОД
угол АОС = углу ДОВ как вертикальные
⇒ треугольники равны по первому признаку ( по двум сторонам и углу между ними)
АО=ОВ
СО=ОД
угол АОС = углу ДОВ как вертикальные
⇒ треугольники равны по первому признаку ( по двум сторонам и углу между ними)
Приложения:
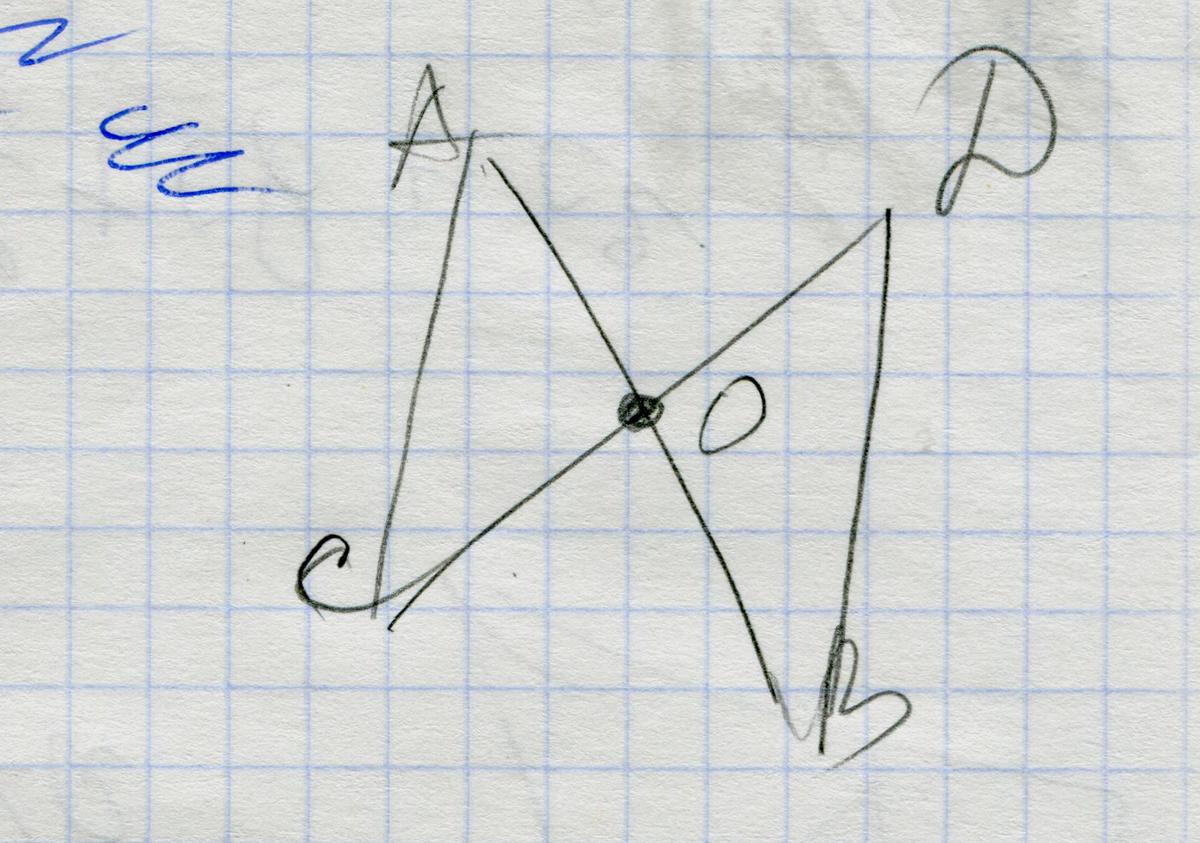
Автор ответа:
0
Т.к. О общая середина, то АО = ОВ и СО =ОД. Т.к. угол АОС и угол ВОД являются вертикальными > они равны. И далее по двум сторонам и углу между ними (АО = ОВ и СО = ОД И угол АОВ равен углу ВОД) Ч.т.д.
Приложения:
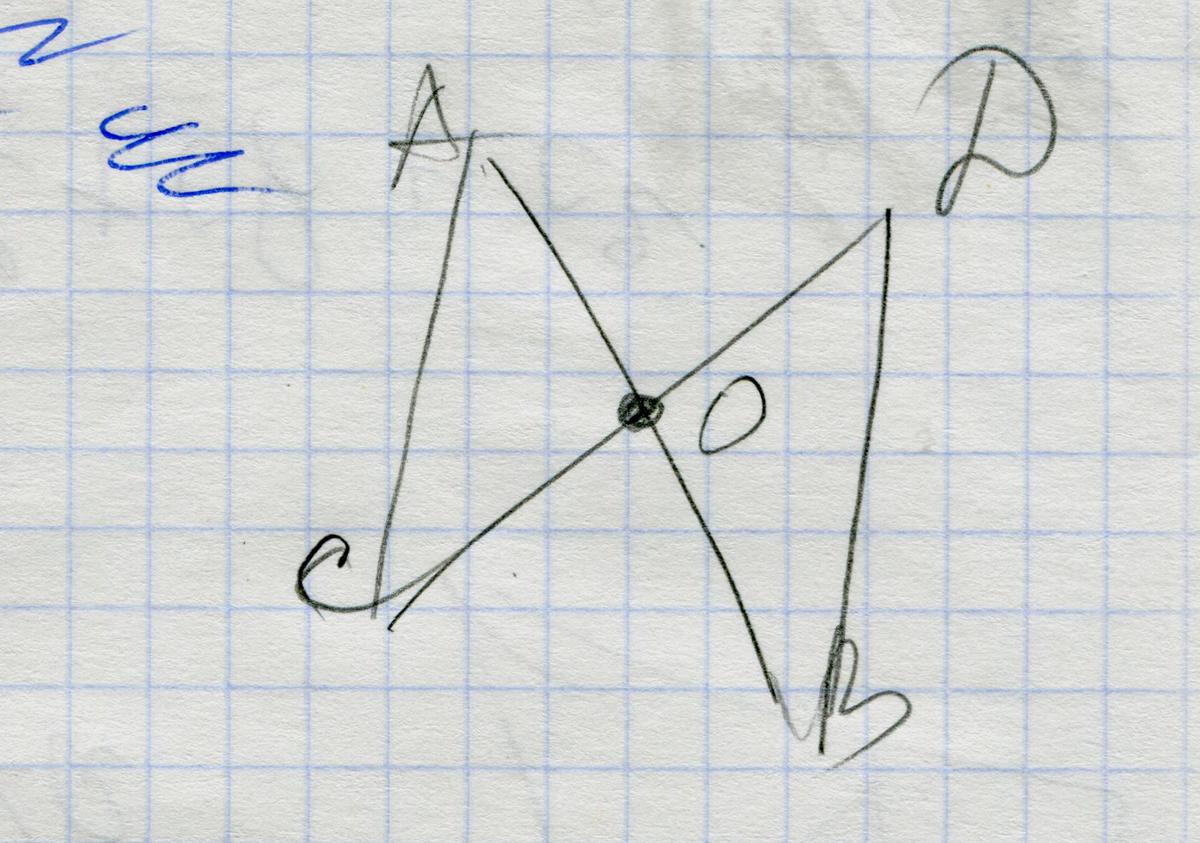
Похожие вопросы
Предмет: Информатика,
автор: ledovskayaanastasia7
Предмет: Математика,
автор: polzovatel455
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: sostavkin
Предмет: География,
автор: Panfilovasofya