Question

Здравствуйте. А предложить другое решение к задаче "Биссектрисы углов B и C трапеции ABCD пересекаются в точке O,лежащей на стороне AD.Докажите,что точка O равноудалена от прямых AB,BC,CD." можно? Если можно, то как?

Answer 1

Расстояние от точки до прямой измеряется перпендикуляром из точки к этой прямой. 
Любая точка биссектрисы угла равноудалена от его сторон. ⇒
расстояние от О до АВ и ВС, сторон угла АВС, равно. 
На том же основании расстояние от О до ВС и СD- равно. 
А так как расстояние от О до ВС равно такому же до АВ и СD, то О- равноудалена от АВ, ВС и CD.
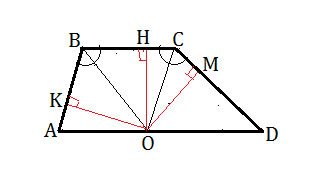
Данное выше свойство биссектрисы доказывается на основании равенства прямоугольных треугольников по общей гипотенузе и острому углу при вершине угла:
Δ ВКО=Δ ВНО;⇒
катеты КО=НО
Δ НСО=Δ МСО⇒
катеты НО=МО. 
Но НО=КО⇒
все три отрезка равны между собой.