Предмет: Алгебра,
автор: tanyasokolova4
Помогите пожалуйста!
Приложения:
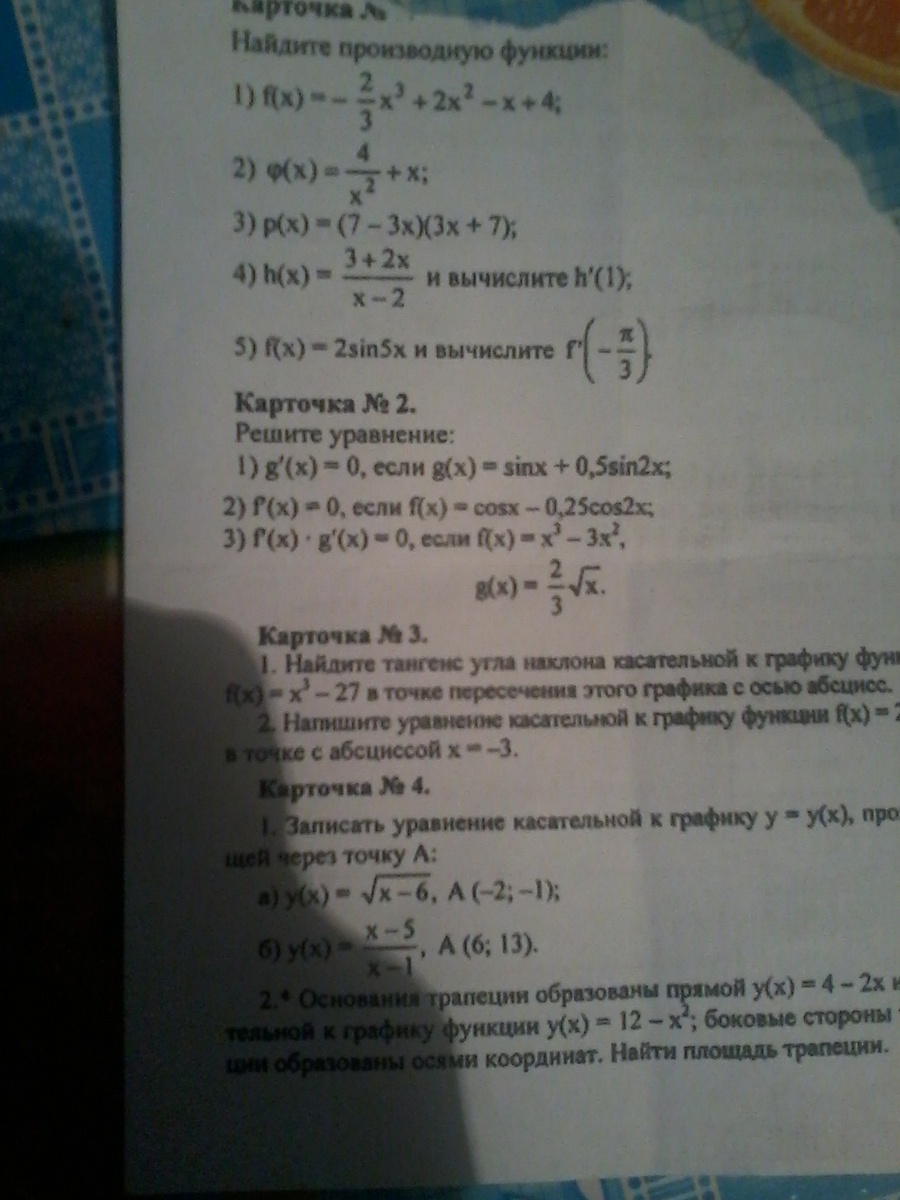

Ответы
Автор ответа:
0
Карточка №1.
1) f(x)= -2/3 x³+2x²-x+4
f(x)' = -2x²+4x-1
2) Ф(x)=4/x² +x = 4x⁻² +x
Ф(x)' = -8x⁻³ +1 = 1 - 8
∛x
3) p(x)=(7-3x)(3x+7)=49-9x²
p(x)' = -18x
4) h(x)= 3+2x
x-2
h(x)' =(3+2x)'(x-2) - (3+2x)(x-2)' = 2(x-2)-(3+2x) = 2x-4-3-2x =
(x-2)² (x-2)² (x-2)²
= -7
(x-2)²
h' (1) = -7 = -7
(1-2)²
5) f(x)=2sin5x
f(x)' = 10cos5x
f' (-π/3) = 10cos(-5π/3) = 10cos(5π/3) = 10cos(6π/3 - π/3) =
= 10cos (π/3) = 10*(1/2) =5
Карточка №2.
1) g(x)=sinx+0.5sin2x
g(x)' = cosx+cos2x
cosx+cos2x=0
cosx+cos²x-sin²x=0
cosx+cos²x-1+cos²x=0
2cos²x+cosx-1=0
y=cosx
2y²+y-1=0
D=1+8=9
y₁= -1-3 = -1
4
y₂= -1+3 =1/2
4
При у=-1
cosx=-1
x=π+2πn, n∈Z
При у=1/2
cosx=1/2
x=+ π/3 + 2πn, n∈Z
Ответ: π+2πn, n∈Z
+ π/3+2πn, n∈Z
2) f(x)=cosx-0.25cos2x
f(x)' = -sinx+0.5sin2x
-sinx+0.5sin2x=0
-sinx+0.5*2sinxcosx=0
-sinx+sinxcosx=0
sinx(cosx-1)=0
sinx=0 cosx-1=0
x=πn, n∈Z cosx=1
x=2πn, n∈Z
Ответ: πn, n∈Z
2πn, n∈Z
3) f(x)=x³-3x²
f(x)' =3x²-6x
g(x)=2/3 √x
g(x)' = 2 = 1
3*2√x 3√x
f(x)' * g(x)' =0
(3x²-6x)( 1 ) =0
3√x
ОДЗ: х≠0
3x²-6x=0
3x(x-2)=0
x=0 - не подходит
x-2=0
x=2
Ответ: 2
Карточка №3.
1) f(x)=x³ -27
x₀=3
f(3)=3³-27=0
f(x)'= 3x²
f(3)'=3*3²=27
y=0+27(x-3)=27x-81
tgα=27
Ответ: 27
1) f(x)= -2/3 x³+2x²-x+4
f(x)' = -2x²+4x-1
2) Ф(x)=4/x² +x = 4x⁻² +x
Ф(x)' = -8x⁻³ +1 = 1 - 8
∛x
3) p(x)=(7-3x)(3x+7)=49-9x²
p(x)' = -18x
4) h(x)= 3+2x
x-2
h(x)' =(3+2x)'(x-2) - (3+2x)(x-2)' = 2(x-2)-(3+2x) = 2x-4-3-2x =
(x-2)² (x-2)² (x-2)²
= -7
(x-2)²
h' (1) = -7 = -7
(1-2)²
5) f(x)=2sin5x
f(x)' = 10cos5x
f' (-π/3) = 10cos(-5π/3) = 10cos(5π/3) = 10cos(6π/3 - π/3) =
= 10cos (π/3) = 10*(1/2) =5
Карточка №2.
1) g(x)=sinx+0.5sin2x
g(x)' = cosx+cos2x
cosx+cos2x=0
cosx+cos²x-sin²x=0
cosx+cos²x-1+cos²x=0
2cos²x+cosx-1=0
y=cosx
2y²+y-1=0
D=1+8=9
y₁= -1-3 = -1
4
y₂= -1+3 =1/2
4
При у=-1
cosx=-1
x=π+2πn, n∈Z
При у=1/2
cosx=1/2
x=+ π/3 + 2πn, n∈Z
Ответ: π+2πn, n∈Z
+ π/3+2πn, n∈Z
2) f(x)=cosx-0.25cos2x
f(x)' = -sinx+0.5sin2x
-sinx+0.5sin2x=0
-sinx+0.5*2sinxcosx=0
-sinx+sinxcosx=0
sinx(cosx-1)=0
sinx=0 cosx-1=0
x=πn, n∈Z cosx=1
x=2πn, n∈Z
Ответ: πn, n∈Z
2πn, n∈Z
3) f(x)=x³-3x²
f(x)' =3x²-6x
g(x)=2/3 √x
g(x)' = 2 = 1
3*2√x 3√x
f(x)' * g(x)' =0
(3x²-6x)( 1 ) =0
3√x
ОДЗ: х≠0
3x²-6x=0
3x(x-2)=0
x=0 - не подходит
x-2=0
x=2
Ответ: 2
Карточка №3.
1) f(x)=x³ -27
x₀=3
f(3)=3³-27=0
f(x)'= 3x²
f(3)'=3*3²=27
y=0+27(x-3)=27x-81
tgα=27
Ответ: 27
Похожие вопросы
Предмет: Математика,
автор: ozubova87
Предмет: Русский язык,
автор: ulbosynsalabaeva
Предмет: Математика,
автор: shkilnik229
Предмет: Математика,
автор: igewschhd
Предмет: Химия,
автор: SemenSkugarev