Question

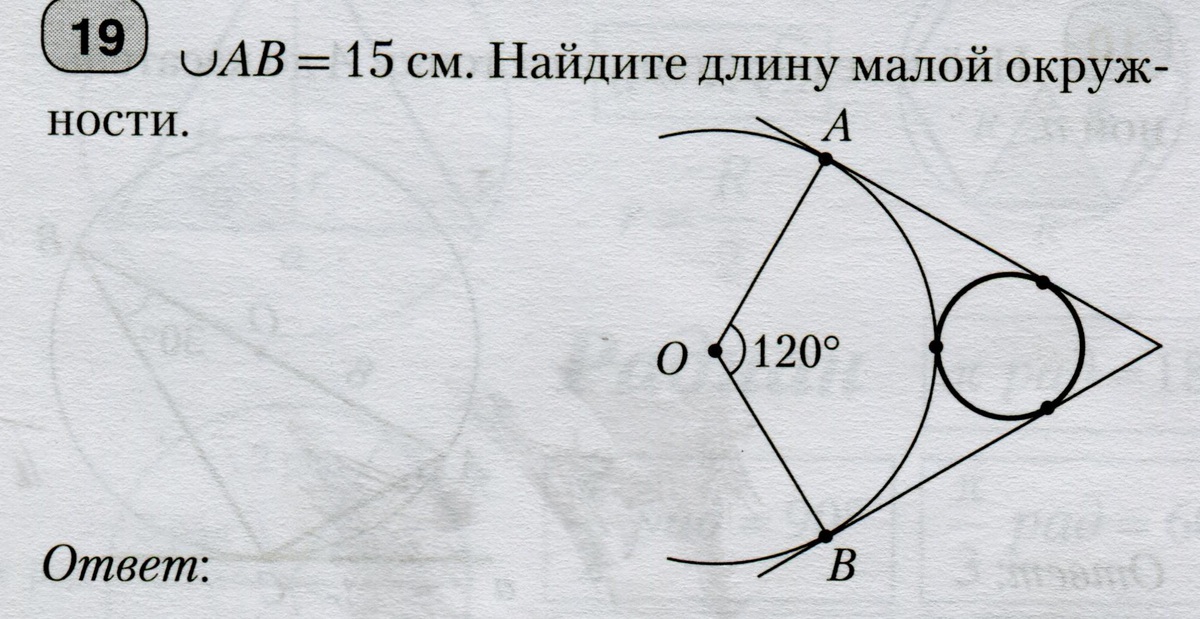
помогите решить, пожалуйста, геометрия 9 класс

Answer 1

Обозначим точку пересечения касательных за С. центр меньшей окружности за О1..
Угол АСО = 90 - (120/2) = 90 - 60 = 30°.
Находим радиус дуги в 120°: $R= frac{180*L}{ pi * alpha } = frac{180*15}{ pi *120} = frac{45}{2* pi }$
Отрезок ОС, лежащий против угла в 30°, равен 2R. 
Отрезок О1С = 2r.
Составим уравнение: ОС = R + r + 2r = R + 3r.
Заменим ОС = 2R.
Тогда 2R = R + 3r.
Или R = 3r.
Отсюда $r= frac{R}{3} = frac{45}{2* pi *3} = frac{15}{2* pi }$.
Длина малой окружности равна:
$l=2 pi r=2 pi * frac{15}{2 pi } =15$см.