Предмет: Математика,
автор: studentkaIRA
Помогите решить, пожалуйста. Безумно срочно нужно
Приложения:
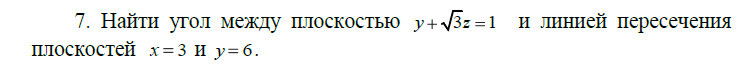
Ответы
Автор ответа:
0
Плоскости x=3 и y=6 при пересечении образуют прямую, параллельную оси OZ.
Для этой прямой образующий вектор единичной длины z=(0;0;1)
Для любой плоскости заданной уравнением Ax+By+Cz+D=0, вектор с координатами (A;B;C) - перпендикулярен этой плоскости.
Для нашего случая для плоскости вектор
является вектором нормали.
Обозначим угол между векторами как
Найдем скалярное произведение вектора нормали и вектора - образующего для прямой пересечения.
Но угол между прямой и плоскостью дополняет угол между прямой и нормалью к плоскости до 90 градусов, т.е.
Ответ: угол между плоскостью и прямой равен
Автор ответа:
0
спасибо вам огромное, Вы мой спаситель!
Похожие вопросы
Предмет: Биология,
автор: Аноним
Предмет: История,
автор: shugylazharasova
Предмет: Математика,
автор: aigerimkuandykova91
Предмет: Алгебра,
автор: Ничка2012
Предмет: Геометрия,
автор: saranadasha