Предмет: Геометрия,
автор: millioner95
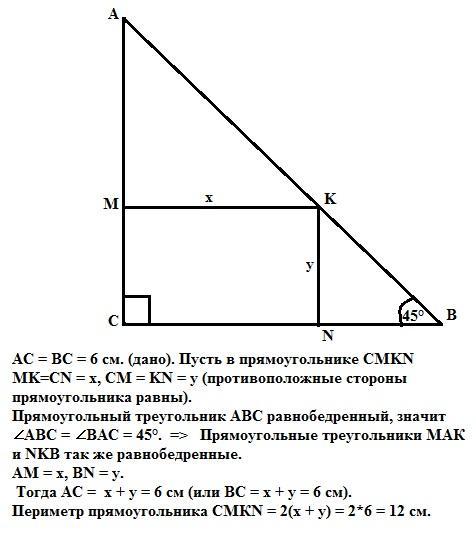
СРОЧНО!!! Геометрия!!! В треугольнике ABC известно, что угол C=90 градусов, AC=BC=6 см. Прямоугольник CMKN построен так,
что точка M принадлежит катету AC, точка N - катету BC, а точка K - гипотенузе AB. Найдите периметр прямоугольника CMKN.
Ответы
Автор ответа:
0
Ответ:
Pcmkn = 12 см.
Объяснение:
АС = ВС = 6 см. (дано). Пусть в прямоугольнике CMKN
MK = CN = x, CM = KN = y (противоположные стороны прямоугольника равны).
Прямоугольный треугольник АВС равнобедренный, значит
∠АВС = ∠ВАС = 45°. => Прямоугольные треугольники МАК и NKB так же равнобедренные и АМ = x, BN = y.
Тогда АС = x + y = 6 см (или ВС = x + y = 6 см).
Периметр прямоугольника СМКN = 2(x + y) = 2*6 = 12 cм.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: aaliyarov3
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: Diana09072009
Предмет: Математика,
автор: dulkina82
Предмет: Химия,
автор: Наташшша