Question

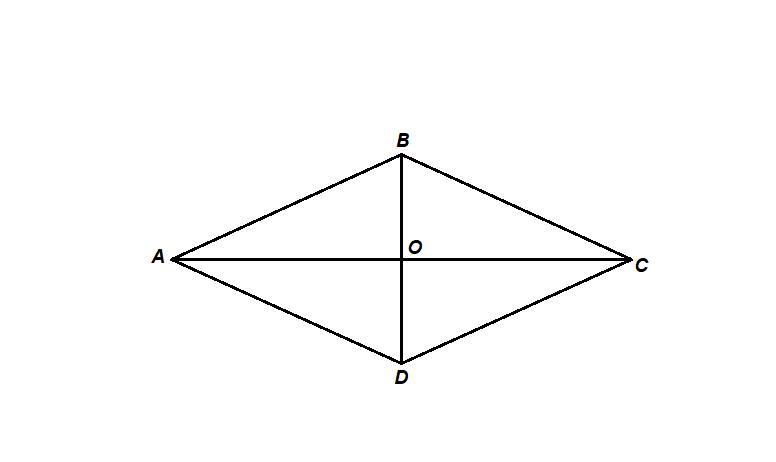
найдите площадь и периметр ромба,если его диагонали равны 10 и 12см

Answer 1

S=(AC*BD)/2

S=(12*10)/2=120/2=60см^

P=4*AB( у ромба все стороны равны)

диагонали ромба делятся пополам, отсда BO=OD=5 , AO=OC=6

Рассмотрим треугольник AOB угол O = 90 градусов отсюда по теореме пифагора

5^2+6^2=61, AB=квадратный корень из 61

P= 4*квадратный корень из 61

Answer 2

Ответ:   S = 60 см²,   Р = 4√61 см

Объяснение:

BD = 10 см, АС = 12 см.

Площадь ромба равна половине произведения диагоналей:

S = (AC · BD) / 2 = (12 · 10) / 2 = 60 см²

Диагонали ромба перпендикулярны и точкой пересечения делятся пополам:

АО = 1/2 АС = 6 см

ВО = 1/2 BD = 5 см

∠АОВ = 90°.

Из прямоугольного треугольника АОВ по теореме Пифагора:

АВ = √(АО² + ВО²) = √(36 + 25) = √61 см

Периметр ромба:

P = 4 · AB = 4√61 см