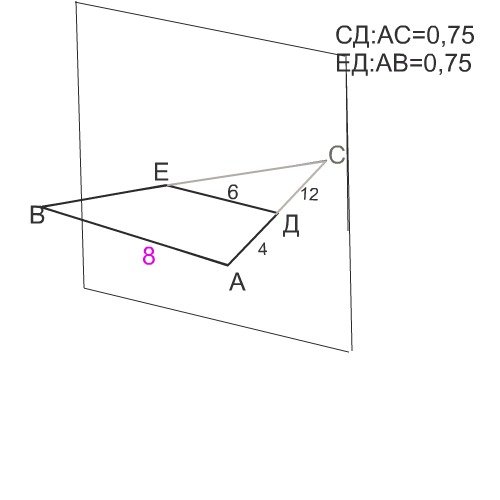
1 задача. Плоскость, параллельная стороне АВ треугольника АВС, пересекает его стороны АС и ВС в точках Д и Е, соответственно. Найти длину стороны АВ, если ДЕ=6см, АД=4см и СД=12см. 2 задача. Из точки к плоскости проведены две наклонные, длины которых равны 27см и 29см, а их проекции относятся как 3:4. Найти проекции наклонных.
Ответы
Решение дано в картинках.
Пояснение:
Треугольники в первой задаче подобные, коэффициент подобия находят отношением
СД:АС=0,75
АВ=6:0,75=8 см
----------------
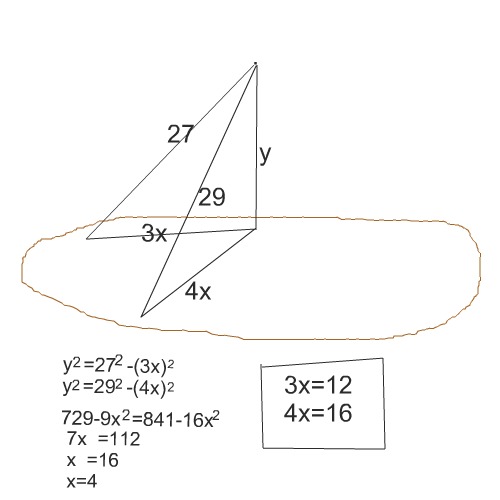
Вторая задача (полное решение во вложении):
Проекции находят из прямоугольных треугольников, один из катетов в которых общий.
Приняв проекции за 3х и 4х ( так как они относястя друг к другу как 3:4), из каждого треугольника найдем квадрат этого общего катета и приравняем уравнения.
В итоге найдем
х=4
Проекция меньшей наклонной равна 12см, большей -16 см.