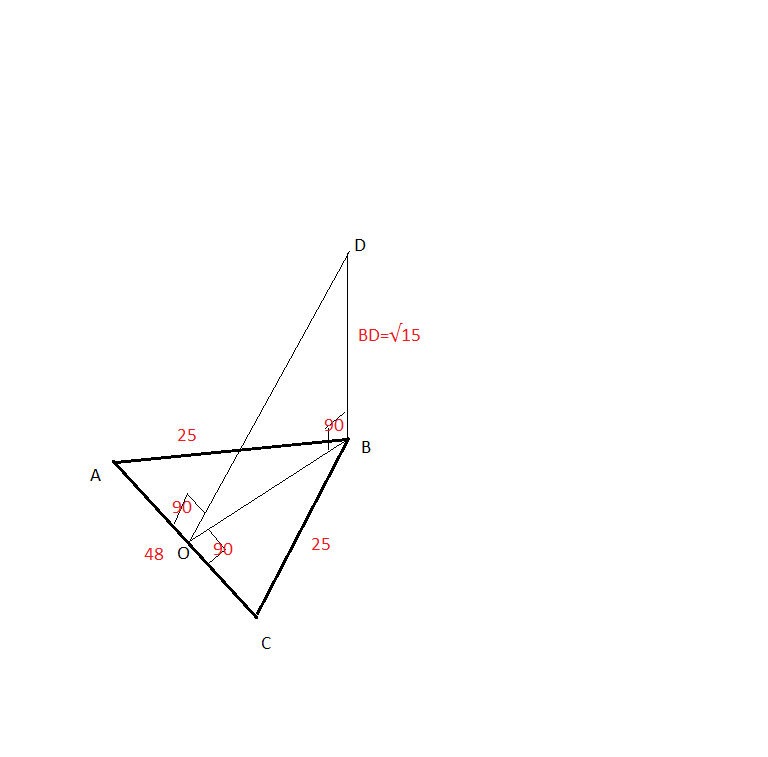
4.В треугольнике АВС : АВ=ВС=25 , АС=48, BD –перпендикуляр к плоскости АВС., BD=√15. Найдите расстояние от точки D до прямой AC.
Ответы
АВ=ВС=25 - треугольник равнобедренный АВ; ВС - боковые стороны
АС=48 - основание
Построим высоту ВК – в равнобедренном треугольнике высота совпадает с медианой
И делит противоположную сторону пополам.
Тогда по теореме Пифагора
BK^2 =AB^2 – (AC/2)^2=25^2-(48/2)^2=49
Высота ВК=7
Расстояние от точки D до прямой AC - обозначим DK – это перпендикуляр/наклонная.
Проекция этой наклонной – высота BK в треугольнике ABC.
По теореме о трех перпендикулярах – треугольник BDK – прямоугольный - < KBD=90 град
Тогда по теореме Пифагора
DK^2 =BK^2 +BD^2 = 7^2 +(√15)^2 =64
DK = 8
Ответ 8
сделаем построение по условию
BD - перпендикуляр
ВО - высота к основанию АС в треугольнике АВС
DO - перпендикуляр к основанию АС
ВО - проекция наклонной DO на плоскость АВС
отрезки DB,BO,OD лежат в одной плоскости и образуют прямоугольный треугольник
треугольник АВС равнобедренный , так как АВ=ВС
высота,медиана,биссектирса совпадают ОС=АС/2=48/2=24
найдем ВО=√(ВС^2-OC^2)=√(25^2-24^2)=7
найдем DО=√(DВ^2+BO^2)=√(√15^2+7^2)=8 <--расстояние от точки D до прямой AC.