Предмет: Алгебра,
автор: Дианка99
Помогите, пожалуйста, упростить выражение с корнями
Приложения:
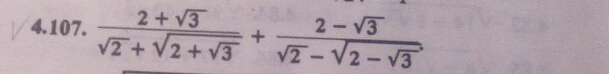
Ответы
Автор ответа:
0
Избавляемся от иррациональности в знаменателях:





Похожие вопросы
Предмет: История,
автор: name3690531
Предмет: Қазақ тiлi,
автор: dosalykamila881
Предмет: Окружающий мир,
автор: 272763738282727
Предмет: История,
автор: Ласка1112
Предмет: Алгебра,
автор: frushka1