Question

Верно ли, что:
1. Сумма углов выпуклого четырехугольника равна 360 .
2. В трапеции углы при каждом основании равны.
3. Квадрат – это параллелограмм, у которого все углы прямые.
4. Вершины А и С ромба ABCD симметричны относительно прямой BD.
5. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные им отрезки.
6. Отрезок, соединяющий точки, лежащие на боковых сторонах трапеции, параллелен основаниям и равен их полусумме.
7. Параллелограмм, у которого все углы равны и все стороны равны, является квадратом.
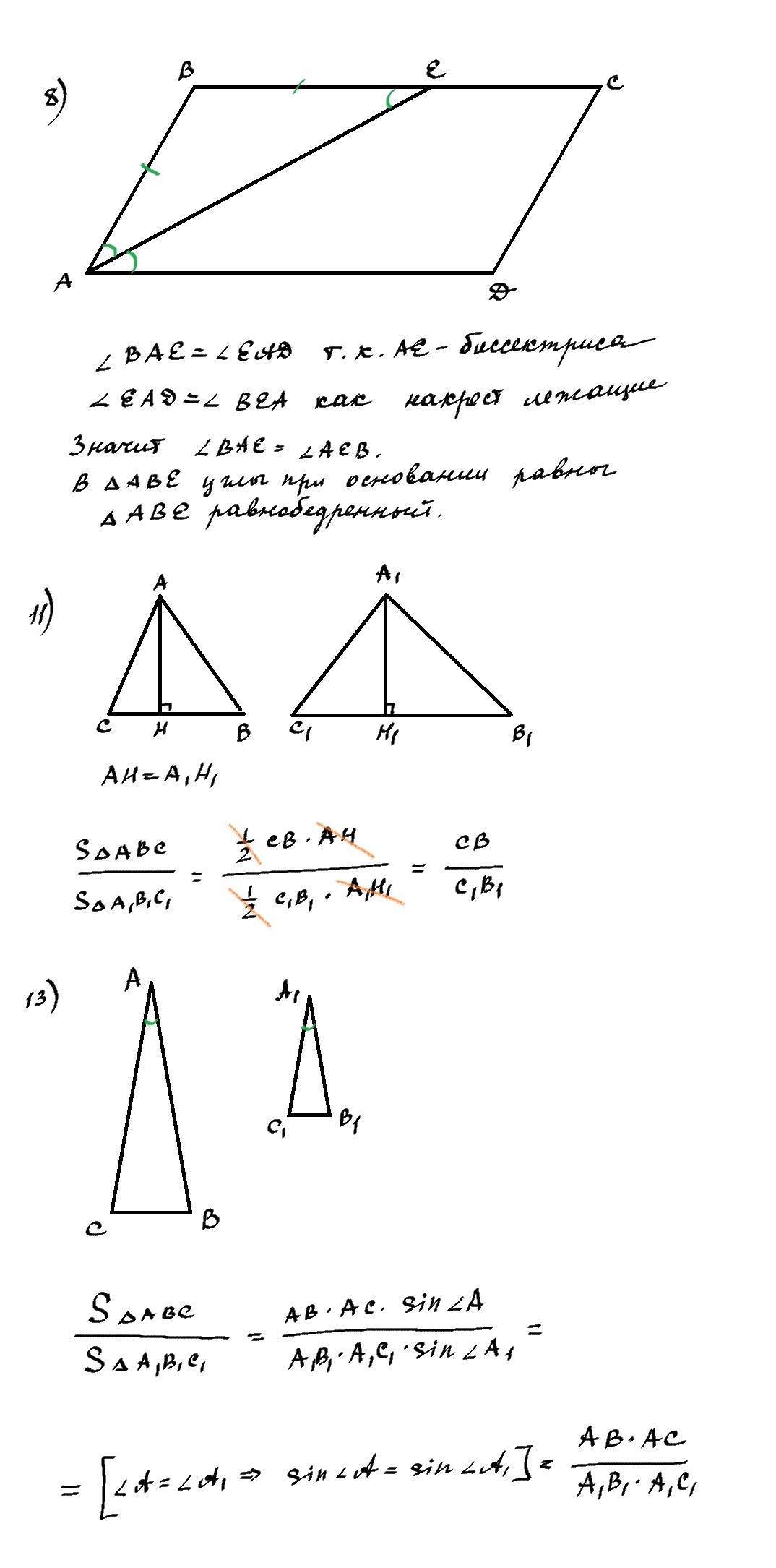
8. Биссектриса одного из углов параллелограмма отсекает от него равнобедренный треугольник.
9. Площадь прямоугольной трапеции равна произведению ее средней линии на боковое ребро.
10. Площадь ромба равна половине произведения его диагоналей на синус угла между ними.
11. Если в треугольниках АВС и А1 В1 С1 высоты АН и А1 Н1 равны, то Sabc:Sa1b1c1= BC:B1C1
12. Площадь прямоугольного треугольника равна произведению его катетов.
13. Если в треугольнике АВС стороны равны 5, 6, 7 см, то его площадь равна $sqrt{18-(18-5)(18-6)(18-7)$ см₂
14. Если в треугольниках АВС и А1В1С1 угол А= угол А1, то S ABC: SA1B1C1=(AB·AC):(A1B1· A1C1)
15. Медианы треугольника делят треугольник на шесть равновеликих треугольников.

Answer 1

1. Верно.
Есть теорема: сумма уголв выпуклого n-угольника равна 180°·(n-2). У четырехугольника 4 угла. Подставляем: 180°·(4-2)=180·2=360°.

2. Неверно.
Углы при основании равны только у равнобедренной трапеции.

3. Неверно.
У квадрата не только все углы прямые, но и все стороны равны.

4. Верно.
ВD - диагональ. Она является осью симметрии ромба.

5. Верно.
При таком построении получаются параллелограммы, т. к. противоположные стороны параллельны. А противоположные стороны в параллелограмме не только параллельны, но и равны.

6. Неверно.
Где расположены эти точки неизвестно, поэтому отрезок, соединяющий их может располагаться под разными углами по отношению к основаниям трапеции.
Отрезок же параллельный основаниями и равный полусумме оснований называется средней линией трапеции и соединяет середины боковых сторон трапеции.

7.Верно.
Параллелограмм - это четырехугольник, значит сумма всех углов равна 360°. Все углы равны: 360°:4=90°. Т. е. получаем четырехугольник, у которого все углы прямые. Кроме этого все стороны равны. Значит это квадрат.

8. Верно (см. рисунок).

9. Неверно.
Площадь трапеции равна произведению средней линии на высоту. В прямоугольной трапеции только одна боковая сторона перпендикулярна основаниям. Поэтому так обобщать мы не можем.

10. Верно.
Площадь любого выпуклого четырехугольника можно вычислить как половина произведения диагоналей, умноженная на синус острого угла между ними.
В ромбе же диагонали пересекаются под прямым углом. Синус 90° равен единице, которая на произведение никак не влияет. Поэтому говорят, что площадь ромба равна половине произведения диагоналей.

11. Верно (смотри вложенный файл).

12. Неверно.
Площадь прямоугольного треугольника равна половине произведения его катетов.

13. Неверно.
Используется формула Герона. Под корнем произведение полупериметра на разности полупериметра и его сторон.$sqrt{18*(18-5)*(18-6)(18-7)}$

14. Верно (смотри вложенный файл)

15. Верно.
Теорема: медианы треугольника делят треугольник на 6 равновеликих треугольников.
Равновеликие треугольники - это треугольники, площади которых равны.