Предмет: Алгебра,
автор: irenon
определите, сколько решений имеет система уравнений x^2 +y^2=25 x^2-y=-5 помогите пожалуйста
Ответы
Автор ответа:
0
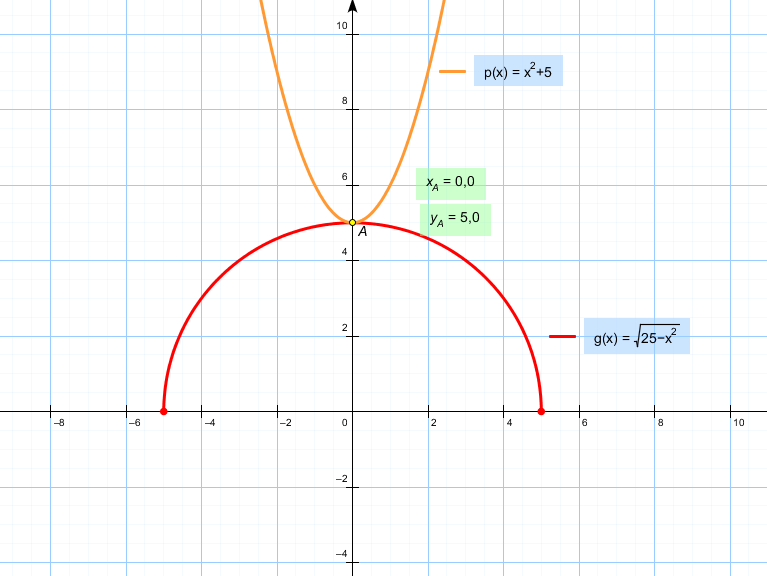
Решим систему уравнений графически.
На рисунке видно, что графики имеют только одну общую точку А(0;5) с координатами х= 0 ; у = 5
Ответ:
система уравнений имеет одно решение
На рисунке видно, что графики имеют только одну общую точку А(0;5) с координатами х= 0 ; у = 5
Ответ:
система уравнений имеет одно решение
Приложения:
Автор ответа:
0
х² + у² = 25 . На координатной плоскости это уравнение графически имеет вид окружности с центром в начале координат и радиуса = 5
х² - у = -5 ⇒ у = х² + 5
у = х² + 5 - это парабола , у которой вершина в точке (0;5). Ветви её вверх. Эта парабола с окружность. имеет одну общую точку ( 0;5)
х² - у = -5 ⇒ у = х² + 5
у = х² + 5 - это парабола , у которой вершина в точке (0;5). Ветви её вверх. Эта парабола с окружность. имеет одну общую точку ( 0;5)
Приложения:

Похожие вопросы
Предмет: Математика,
автор: atrubina110
Предмет: Русский язык,
автор: dimamort17
Предмет: Биология,
автор: arafatprimbetov0
Предмет: История,
автор: AHHA123