постройте график функции у=(х2+1)(х+2)/ -2-х и определите при каких значениях К прямая у=кх имеет с графиком ровно одну общую точку. SOS.
Ответы
Область определения -2-x≠0 ⇒ x≠-2
D(y) : x ∈ (-∞; -2) ∪ (-2; +∞)
y = - x² - 1; x ≠ -2
График функции - квадратичная парабола, ветви направлены вниз.
Координаты вершины из уравнения функции
x₀ = 0; y₀ = -1
y = kx - прямая, проходящая через начало координат.
-x² - 1 = kx ⇔ x² + kx + 1 = 0
Квадратное уравнение имеет один корень, когда D = 0.
D = k² - 4 = 0 ⇔ k² = 4
k₁ = 2; k₂ = -2
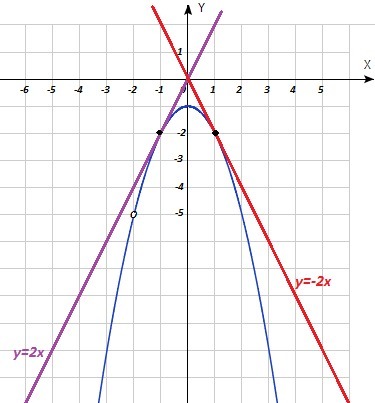
1) 2x = -x² - 1 ⇔ x² + 2x + 1 = 0 ⇔ (x + 1)² = 0
x = -1; y = 2x = 2·(-1) = -2
Прямая y = 2x имеет с параболой одну общую точку (-1; -2)
2) -2x = -x² - 1 ⇔ x² - 2x + 1 = 0 ⇔ (x - 1)² = 0
x = 1; y = -2x = -2·1 = -2
Прямая y = -2x имеет с параболой одну общую точку (1; -2)
Ответ : k₁ = 2; k₂ = -2