Question

Пользуясь геометрическим смыслом определённого интеграла,вычислите:
$intlimits^6_0 {|x-3|} , dx$

Answer 1

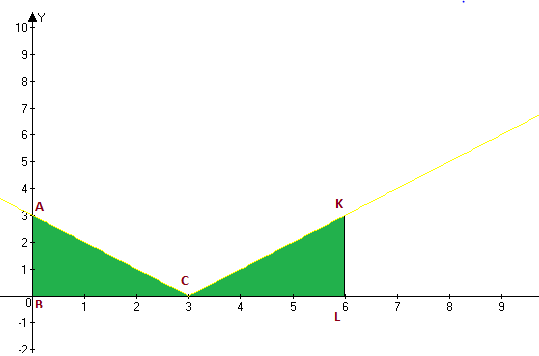
Построим график функции f(x)=|x-3|
   План построения графика:
1) Строим f(x)=x-3, прямую проходящую через точки (0;-3), (3;0)
2) Нижнюю часть графика f(x)=x-3, отобразить относительно оси Ох и получим график функции f(x)=|x-3|
  
На графике отметим ограченные линии [0;6]. Видим что они образуют прямоугольные треугольники с катетами 3.

Площадь фигуры ограниченными линиями будет сумма площадей прямоугольных треугольников.
  Назовём первый треугольник ARC, а другой - KLC
Площадь ARC = AR*RC = 3*3 = 9 кв. ед.
Площадь KLC = KL * LC = 3*3 = 9 кв. ед.

Площадь ограниченной фигуры: S=S₁+S₂=9+9 = 18 кв.ед. 

Ответ: 18.