Предмет: Алгебра,
автор: 0917alena369
Решительно только что в кружочках! Даю 37 баллов очень срочно!!!!!
Приложения:
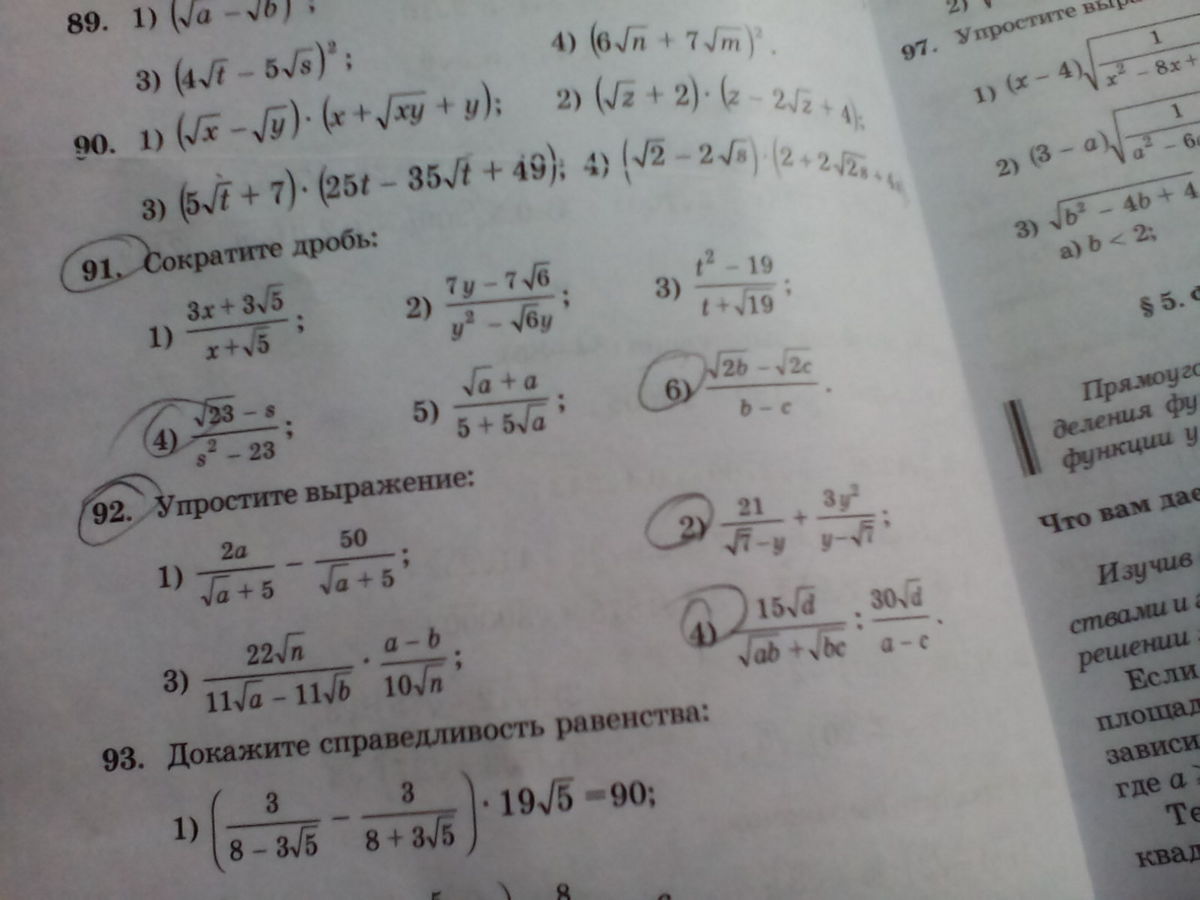
Ответы
Автор ответа:
0
Автор ответа:
0
решение в приложении.
Приложения:
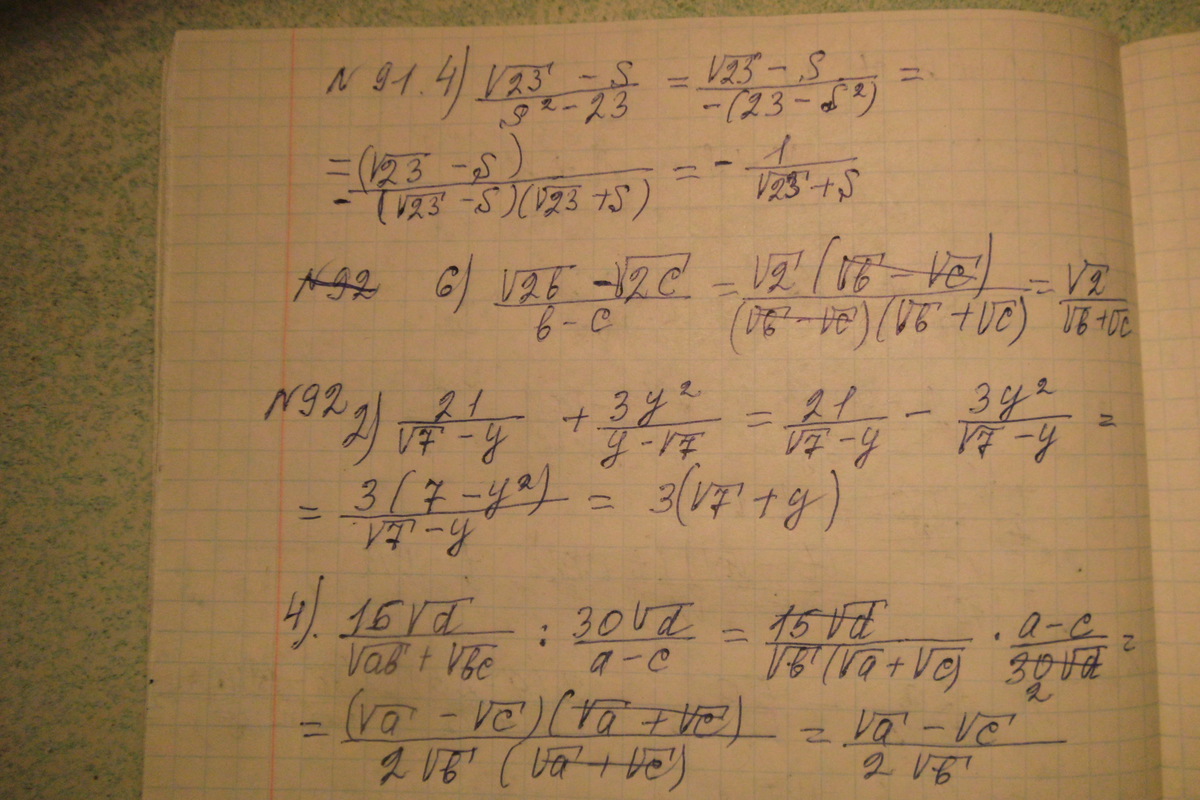
Похожие вопросы
Предмет: Геометрия,
автор: Provokatsiya
Предмет: Литература,
автор: Dimashkesikbaev20109
Предмет: Математика,
автор: rayhonsadirdinova
Предмет: Алгебра,
автор: gasya98
Предмет: Математика,
автор: димос66