Question

около правильного треугольника описана окружность радиуса R. докажите что R=2r, где r радиус окружности вписанной в этот треугольник.

Answer 1

Около правильного треугольника описана окружность радиуса R. докажите что R = 2r, где r - радиус окружности, вписанной в этот треугольник.

=============================================================

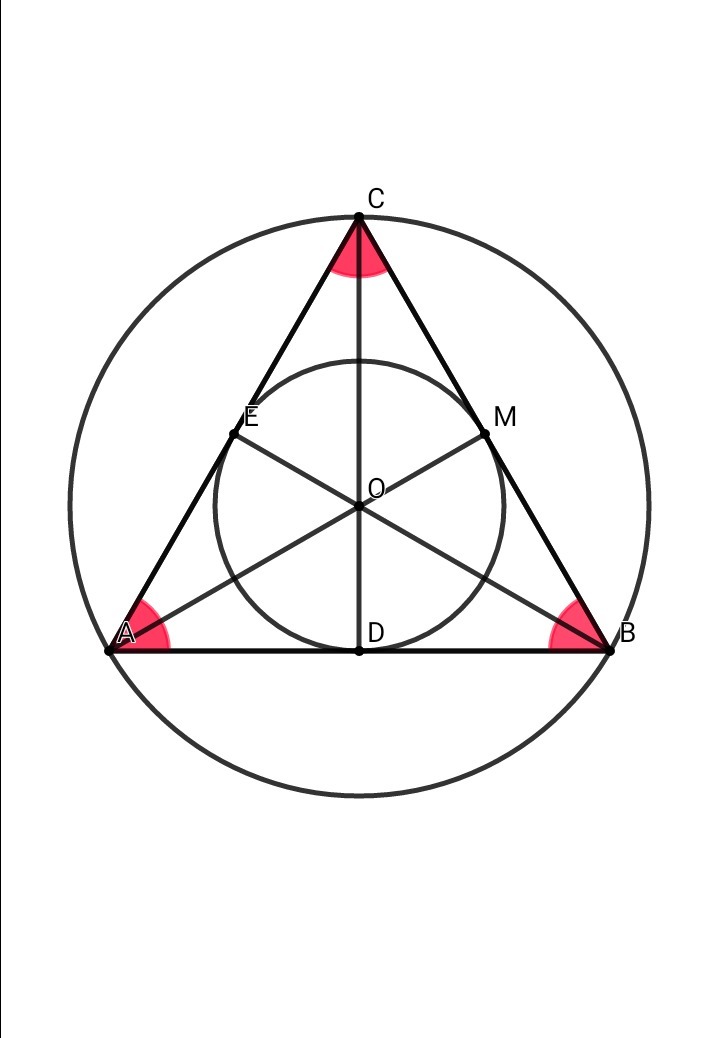
В правильном треугольнике высоты, медианы и биссектрисы совпадают: АМ = BE = CD. Соответственно, совпадают и центры описанной и вписанной окружности. Центром описанной окружности является точка пересечения серединных перепендикуляров, то есть высоты данного треугольника ⇒ АО = ВО = СО = R . Центром вписанной окружности является точка пересечения биссектрис, то есть биссектрисы данного треугольника ⇒ OE = OM = OD = r.

Так как AM = BE = CD - медианы ΔАВС  ⇒

Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2:1, считая от вершины.

Значит, СО:ОD = 2:1  ⇒ R:r = 2:1 ⇒ R = 2r, что и требовалось доказать.