Предмет: Геометрия,
автор: Mendozz
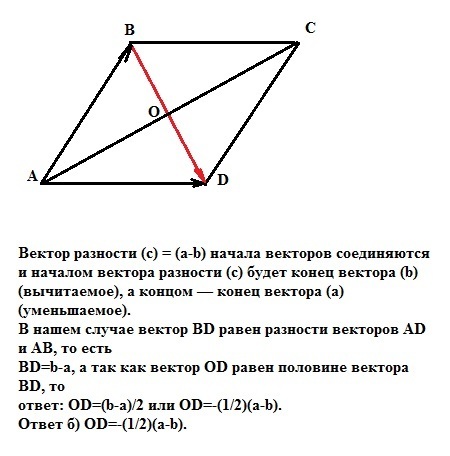
В параллелограмме ABCD диагонали пересекаются в точке O. Выразить через векторы a = AB и b = AD вектор OD.
Ответы: a) OD = 1/2(a-b); б) OD = -1/2(a-b); в) OD = 1/2(a+b).
Ответы
Автор ответа:
0
Вектор разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
В нашем случае вектор BD равен разности векторов AD и AB, то есть
BD=b-a, а так как вектор ОD равен половине вектора BD, то
ответ: OD=(b-a)/2 или OD=-(1/2)(a-b).
Ответ б) OD=-(1/2)(a-b).
В нашем случае вектор BD равен разности векторов AD и AB, то есть
BD=b-a, а так как вектор ОD равен половине вектора BD, то
ответ: OD=(b-a)/2 или OD=-(1/2)(a-b).
Ответ б) OD=-(1/2)(a-b).
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: denismihalcuk98
Предмет: Русский язык,
автор: Dobra9l
Предмет: Алгебра,
автор: ler61
Предмет: Математика,
автор: salman04042000
Предмет: Алгебра,
автор: Марго19981998