Question

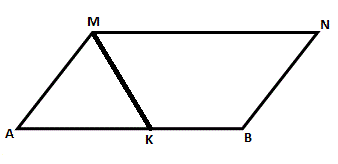
Дано: AMNB - параллелограмм
AM=MK, <AMK=60o , MK=3 cm, KB=4 cm

Найти: Периметр AMNB.

Answer 1

Так как АМ=МК(по усл.), то ΔАМК - равнобедренный(по опр.)⇒АМ=МК=3.
Если ∠М=60, а ∠МАК=∠МКА(по св-ву равнобедр. Δ), мы можем найти  ∠МАК и∠МКА посредством теоремы о сумме углов треугольника(сумма ∠ Δ равна 180)
$frac{180 - 60}{2}$=60
Получим: так как все углы Δ МАК равны 60, то этот треугольник является равносторонним(по признаку) ⇒ АК=МА=МК=3(по опр. равностор. Δ)
Значит большие стороны равны 3+4=7, а меньшие равны 3
Найдем периметр: 14+6=20

Answer 2

Спасибо :)