Найдите производную функцию у= f (x) в точке х=1
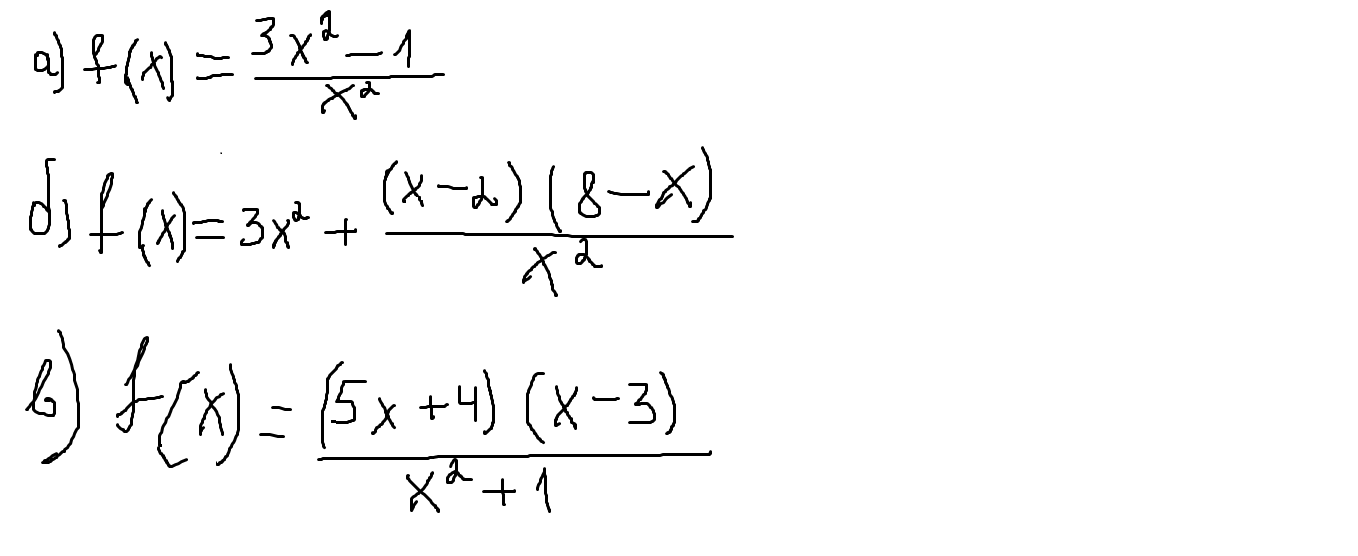
Ответы
f '(x) = ((3x²-1) / x²)' = (6x*x² - 2x(3x²-1)) / x⁴ = (6x³-6x³+2x) / x⁴ = 2x/x⁴ = 2/x³
f '(1) = 2/1³ = 2
f ' (x) = (3x²)' + ((x-2)(8-x) / x²)' = 6x + ((8x-16-x²+2x) / x²)' = 6x -((x²-10x+16) / x²)' = 6x - ((2x-10)x² - 2x(x²-10x+16)) / x⁴ = 6x - (2x³-10x²-2x³+20x²+32x) / x⁴ = 6x - (10x²+32x) / x⁴ = 6x - (x(10x+32)) / x⁴ = 6x - (10x+32)/x³
f '(1) = 6*1 - (10*1 +32) / 1³ = 6 -42 = -36
f '(x) = ((5x²+4x-15x-12) / (x²+1))' = ((5x²-11x-12) / (x²+1))' = ((10x-11)(x²+1) - 2x(5x²-11x-12)) / (x²+1)² = (10x³-11x²+10x-11-10x³+22x²+24x) / (x²+1)² = (11x²+34x-11) / (x²+1)²
f '(1) = (11+34-11) / 2² = 34/4 =17/2 = 8.5
1) f '(x) = ((3x²-1) / x²)' = (6x*x² - 2x(3x²-1)) / x⁴ = (6x³-6x³+2x) / x⁴ = 2x/x⁴ = 2/x³
f '(1) = 2/1³ = 2
2) f ' (x) = (3x²)' + ((x-2)(8-x) / x²)' = 6x + ((8x-16-x²+2x) / x²)' = 6x -((x²-10x+16) / x²)' = 6x - ((2x-10)x² - 2x(x²-10x+16)) / x⁴ = 6x - (2x³-10x²-2x³+20x²+32x) / x⁴ = 6x - (10x²+32x) / x⁴ = 6x - (x(10x+32)) / x⁴ = 6x - (10x+32)/x³
f '(1) = 6*1 - (10*1 +32) / 1³ = 6 -42 = -36
3) f '(x) = ((5x²+4x-15x-12) / (x²+1))' = ((5x²-11x-12) / (x²+1))' = ((10x-11)(x²+1) - 2x(5x²-11x-12)) / (x²+1)² = (10x³-11x²+10x-11-10x³+22x²+24x) / (x²+1)² = (11x²+34x-11) / (x²+1)²
f '(1) = (11+34-11) / 2² = 34/4 =17/2 = 8.5