Предмет: Алгебра,
автор: locer
Пожалуйста выполните все во вложении, очень прошу))))
Приложения:
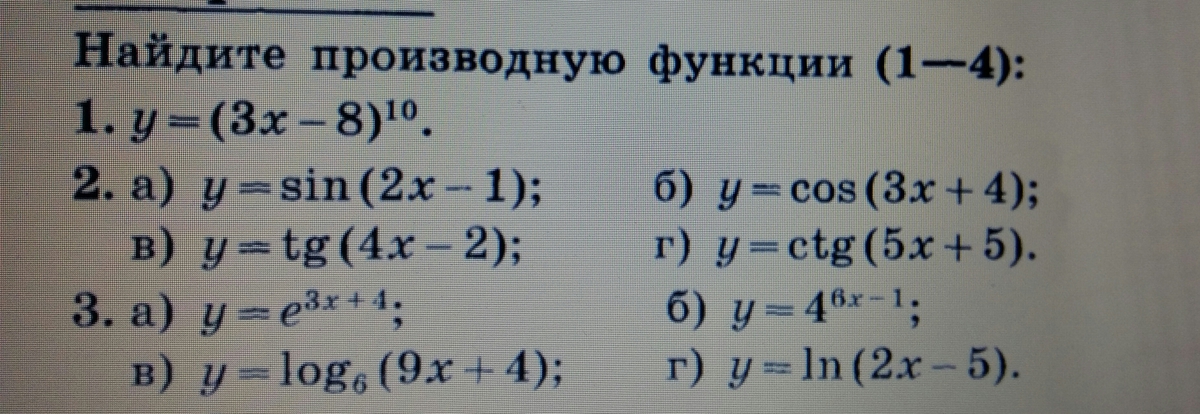
Ответы
Автор ответа:
0
Все задания на вычисление производной сложной функции:
F(g(x))`=F`(g(x))· g`(x)
1. y=(3x-8)¹⁰
Обозначения:
g(x)=3x-8
F(g(x))=(g(x))¹⁰
Поэтому F`(g(x))=10·(g(x))⁹·g`(x)
Само решение выглядит так:
y`=10(3x-8)⁹·(3x-8)`=10·(3х-8)⁹·3=30·(3х-8)⁹
2. 1) у`=(sin(2x-1))`=cos(2x-1)·(2x-1)`=cos(2x-1)·2=cos(2x-1)
2) у`=(cos(3x+4))`=-sin(3x+4)·(3x+4)`=-sin(3x+4)·3=-3sin(3x+4)






F(g(x))`=F`(g(x))· g`(x)
1. y=(3x-8)¹⁰
Обозначения:
g(x)=3x-8
F(g(x))=(g(x))¹⁰
Поэтому F`(g(x))=10·(g(x))⁹·g`(x)
Само решение выглядит так:
y`=10(3x-8)⁹·(3x-8)`=10·(3х-8)⁹·3=30·(3х-8)⁹
2. 1) у`=(sin(2x-1))`=cos(2x-1)·(2x-1)`=cos(2x-1)·2=cos(2x-1)
2) у`=(cos(3x+4))`=-sin(3x+4)·(3x+4)`=-sin(3x+4)·3=-3sin(3x+4)
Похожие вопросы
Предмет: МХК,
автор: JoniCadomaza
Предмет: История,
автор: den2281337228133761
Предмет: Литература,
автор: Zat7es
Предмет: История,
автор: kirill968