Предмет: Математика,
автор: Galyaboos1
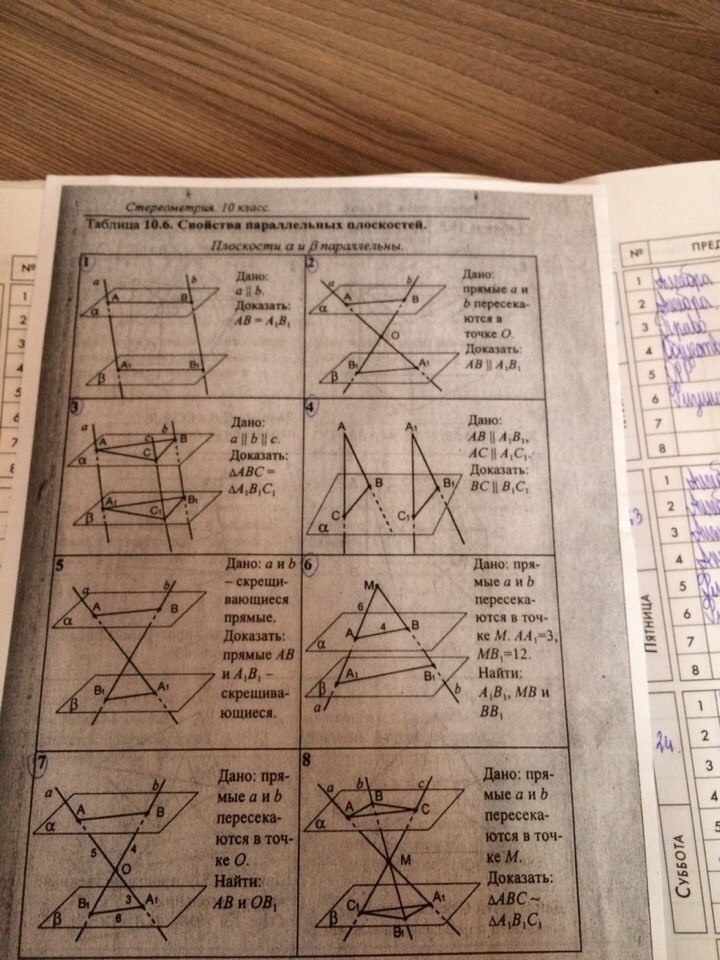
Помогите пожалуйста сделать задачи номера 1,2,3,4,6,7
Приложения:
Ответы
Автор ответа:
0
Признак параллельности плоскостей.Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
1)a || b по условию. Значит АА₁ и ВВ₁ лежат в одной плоскости.
По теореме 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Значит АВ || A₁B₁. Значит АВВ₁А₁ параллелограмм, у него противоположные стороны параллельны. А раз АВВ₁А₁ параллелограмм, то АВ=А₁В₁
2)Две пересекающиеся прямые АА₁ и ВВ₁ лежат в одной плоскости. То есть плоскость АВА₁В₁ пересекается с плоскостями α и β. По теореме 1, если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Значит АВ || A₁B₁.
3)АА₁ и ВВ₁ параллельны, значит они лежат в одной плоскости. Значит по теореме 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Значит АВ и А₁В₁ тоже параллельны. Получается АВВ₁А₁ параллелограмм - противоположные стороны параллельны. Значит АВ=А₁В₁. Аналогично доказывается и равенство других соответственных сторон.
4)По признаку параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Значит плоскость АВС || A₁B₁C₁.
Получается две плоскости АВС и А₁В₁С₁ пересекаются третьей α.
По теореме 1 получается СВ || C₁B₁.
6)Прямые А₁М и В₁М пересекаются в точке М - значит лежат в одной плоскости. По теореме 1 получается АВ || A₁B₁.
Значит треугольники МАВ и МА₁В₁ подобны по двум углам . А₁М/AM=A₁B₁/AB
A₁M=AA₁+AM=9
значит А₁В₁=6
МВ/MB₁=AM/A₁M=2/3
MB=8
7)Прямые АА₁ и ВВ₁ лежат в одной плоскости. Значит по теореме 1 АВ || A₁B₁. Значит треугольники АОВ и ОА₁В₁ подобны по двум углам (ОАВ=ОА₁В₁ , ОВ₁А₁=ОВА).
АО/OA₁=AB/B₁A₁=5/3
AB=12
АО/OA₁=OB/OB₁
OB₁=2,4
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
1)a || b по условию. Значит АА₁ и ВВ₁ лежат в одной плоскости.
По теореме 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Значит АВ || A₁B₁. Значит АВВ₁А₁ параллелограмм, у него противоположные стороны параллельны. А раз АВВ₁А₁ параллелограмм, то АВ=А₁В₁
2)Две пересекающиеся прямые АА₁ и ВВ₁ лежат в одной плоскости. То есть плоскость АВА₁В₁ пересекается с плоскостями α и β. По теореме 1, если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Значит АВ || A₁B₁.
3)АА₁ и ВВ₁ параллельны, значит они лежат в одной плоскости. Значит по теореме 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Значит АВ и А₁В₁ тоже параллельны. Получается АВВ₁А₁ параллелограмм - противоположные стороны параллельны. Значит АВ=А₁В₁. Аналогично доказывается и равенство других соответственных сторон.
4)По признаку параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Значит плоскость АВС || A₁B₁C₁.
Получается две плоскости АВС и А₁В₁С₁ пересекаются третьей α.
По теореме 1 получается СВ || C₁B₁.
6)Прямые А₁М и В₁М пересекаются в точке М - значит лежат в одной плоскости. По теореме 1 получается АВ || A₁B₁.
Значит треугольники МАВ и МА₁В₁ подобны по двум углам . А₁М/AM=A₁B₁/AB
A₁M=AA₁+AM=9
значит А₁В₁=6
МВ/MB₁=AM/A₁M=2/3
MB=8
7)Прямые АА₁ и ВВ₁ лежат в одной плоскости. Значит по теореме 1 АВ || A₁B₁. Значит треугольники АОВ и ОА₁В₁ подобны по двум углам (ОАВ=ОА₁В₁ , ОВ₁А₁=ОВА).
АО/OA₁=AB/B₁A₁=5/3
AB=12
АО/OA₁=OB/OB₁
OB₁=2,4
Похожие вопросы
Предмет: Математика,
автор: wrtjhowrntjonwrj
Предмет: Алгебра,
автор: dbbdhfh5555
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: angelok1976