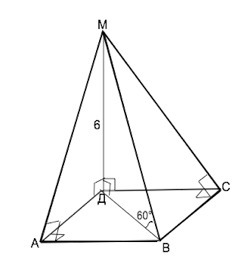
Из точки М проведён перпендикуляр МД,равный 6см,к плоскости квадрата АВСД.Наклонная МВ обрвзует с плоскостью квадрата угол 60 градусов. а)Докажите,что треугольники МАВ и МСВ прямоугольные. б)Найдите сторону квадрата. в)докажите,что треугольник АВД является проекцией треугольника МАВ на плоскость квадрата,и найдите его площадь.
ребяяяяята, пожалуйста решите мне( с объяснениями, мне оченьочень нужно
Ответы
а) ДА⊥АВ, МД⊥(АВСД), АД - проекция МА на плоскость квадрата. По т. о 3-х перпендикулярах МА⊥АВ⇒ ∆ МАВ прямоугольный. Аналогично доказывается, что ∆ МСД прямоугольный.
б) Из ∆ МДВ ДВ=ВД:tg60°=6/√3=2√3
∆ АВД прямоугольный равнобедренный с острыми углами 45°.
АВ=ВД•sin45°=√6
в) АД- проекция АМ, ВД - проекция ВМ,
АВ - общая сторона ∆ МАВ и ∆ АВД, ⇒
∆ АВД является проекцией. ∆ МАВ на плоскость квадрата.
S(АВСД)=(√6)²=6 см² ⇒-
S(МАВ)=Ѕ(АВСД):2=3 см²