Предмет: Алгебра,
автор: borg3008
Помогите решить это задание:
Приложения:
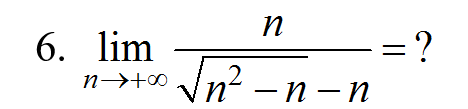
Ответы
Автор ответа:
0
Принцип действий: выносим старшую степень в числителе и знаменателе за скобки, сокращаем и решаем упрощённый предел.
Решение:

* для последовательностей этот момент роли не играет, больше для функций: здесь - , следовательно для достаточно большого
, следовательно для достаточно большого  выполняется
выполняется  , потому можно сократить
, потому можно сократить  .
.
(почему неважно для последовательностей?)
Получили предел:

Решаем:

Решение:
* для последовательностей этот момент роли не играет, больше для функций: здесь -
(почему неважно для последовательностей?)
Получили предел:
Решаем:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Dannnnk
Предмет: Алгебра,
автор: ievghieniiru
Предмет: Химия,
автор: valdespestov