Предмет: Геометрия,
автор: skomolcev
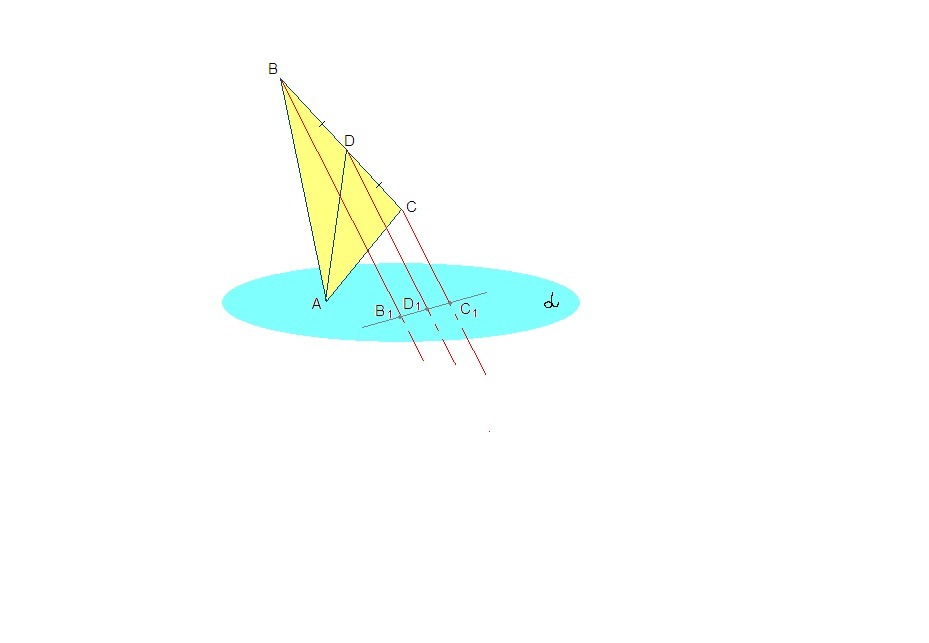
Вершина А треугольника АВС лежит в плоскости а, вершины В и С расположены по одну сторону от этой плоскости. Отрезок АD - медиана треугольника АВС. Через точки B, D, C проведены параллельные прямые, пересекающие плоскость в точках В1, D1, C1 соответственно. Найдите длину DD1, если ВВ1 = 2 см и СС1 = 12 см.
Ответы
Автор ответа:
0
Через прямую ВВ₁ и ВС можно провести единственную плоскость.
Так как точка D лежит на ВС, она лежит в этой плоскости.
DD₁║BB₁ и CC₁║BB₁ значит DD₁ и СС₁ так же лежат в этой плоскости.
Эта плоскость пересекает плоскость α по прямой В₁С₁, значит и точка D₁ лежит на линии пересечения плоскостей.
Итак, В₁ВСС₁ - плоский четырехугольник, у которого две стороны параллельны, т.е. трапеция.
DD₁ параллелен основаниям трапеции и проходит через середину боковой стороны, значит является средней линией.
DD₁ = (СС₁ + ВВ₁)/2 = (12 + 2)/2 = 7 см
Так как точка D лежит на ВС, она лежит в этой плоскости.
DD₁║BB₁ и CC₁║BB₁ значит DD₁ и СС₁ так же лежат в этой плоскости.
Эта плоскость пересекает плоскость α по прямой В₁С₁, значит и точка D₁ лежит на линии пересечения плоскостей.
Итак, В₁ВСС₁ - плоский четырехугольник, у которого две стороны параллельны, т.е. трапеция.
DD₁ параллелен основаниям трапеции и проходит через середину боковой стороны, значит является средней линией.
DD₁ = (СС₁ + ВВ₁)/2 = (12 + 2)/2 = 7 см
Приложения:
Похожие вопросы
Предмет: География,
автор: pupil06v02
Предмет: Русский язык,
автор: adaliabajzomart
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: Аноним
Предмет: Биология,
автор: ьариша