Предмет: Математика,
автор: syasikovao
Помогите пожалуйста решить буквы Ж; Г; Е
Приложения:
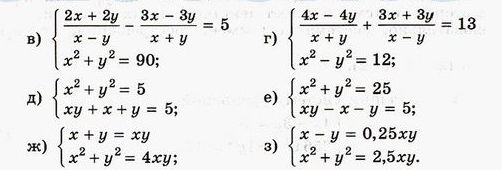
Ответы
Автор ответа:
0
г).
Работаем над первым уравнением:

Получили однородное уравнение, переводим в квадратное и находим связь

Тут мы делили на , следовательно - исключили возможность
, следовательно - исключили возможность  . Этот случай нужно будет проверить отдельно.
. Этот случай нужно будет проверить отдельно.
Получили две связи:

Добавляем к каждой второе уравнение и получаем две простые системы уравнений:

которые решить уже не проблема.
Теперь проверяем частный случай :
:

Равенство не выполняется, значит не является решением системы.
не является решением системы.
е).
Решаем подстановкой:

Решаем простую систему:

Получили две простые системы:

Осталось только найти , что нетрудно сделать.
, что нетрудно сделать.
ж).
Тот же принцип, что и в е).
Приводим к нужному виду второе уравнение:

Назначаем новые переменные:

Подставляем в систему и получаем:

Получили две системы:
Oдна из них - тривиальна
Вторая -
Осталось только посчитать ответы.
Работаем над первым уравнением:
Получили однородное уравнение, переводим в квадратное и находим связь
Тут мы делили на
Получили две связи:
Добавляем к каждой второе уравнение и получаем две простые системы уравнений:
которые решить уже не проблема.
Теперь проверяем частный случай
Равенство не выполняется, значит
е).
Решаем подстановкой:
Решаем простую систему:
Получили две простые системы:
Осталось только найти
ж).
Тот же принцип, что и в е).
Приводим к нужному виду второе уравнение:
Назначаем новые переменные:
Подставляем в систему и получаем:
Получили две системы:
Oдна из них - тривиальна
Вторая -
Осталось только посчитать ответы.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: francesko16
Предмет: Физика,
автор: mekabjapar
Предмет: Русский язык,
автор: akorshunova200729
Предмет: Физика,
автор: Лиза20143
Предмет: География,
автор: anechkaswag