Question

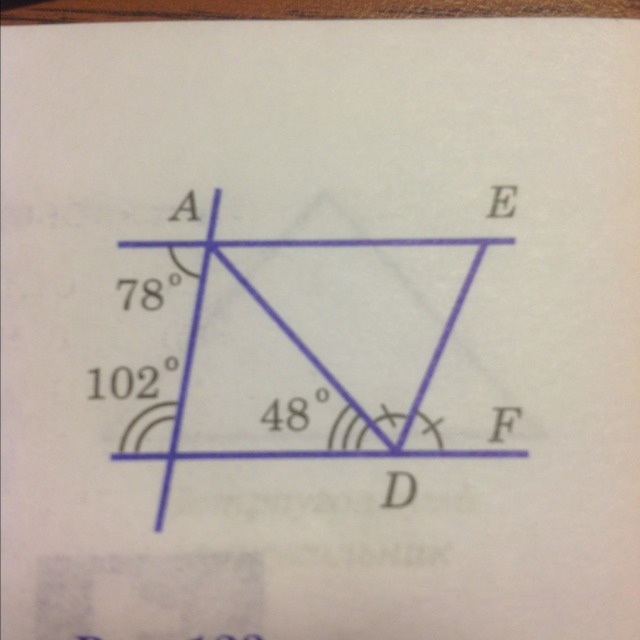
По рисунку. DE биссектриса угла ADF . По данным рисунка найдите углы треугольника ADE

Answer 1

∠САВ + ∠КВА = 78° + 102° = 180°
Эти углы - односторонние при пересечении прямых АЕ и BD секущей АВ, значит АЕ ║ BD.

∠EAD = ∠BDA = 48° как накрест лежащие при пересечении параллельных прямых АЕ и BD секущей AD.

∠ADB и ∠ADF cмежные, их сумма равна 180°, а биссектриса DE делит угол ADF пополам, следовательно:
∠EDA = ∠EDF = (180° - 48°)/2 = 132/2 = 66°.

Сумма углов треугольника 180°:
∠AED = 180° - (∠EDA + ∠EAD) = 180° - (66° + 48°) = 180° - 114° = 66°