Предмет: Алгебра,
автор: BJIADA
1.408,1.410,1.411 под буквами "а"
Приложения:

Ответы
Автор ответа:
0
решение во вложенииииииииииииииииииииии
11 добавлю
добавила
11 добавлю
добавила
Приложения:
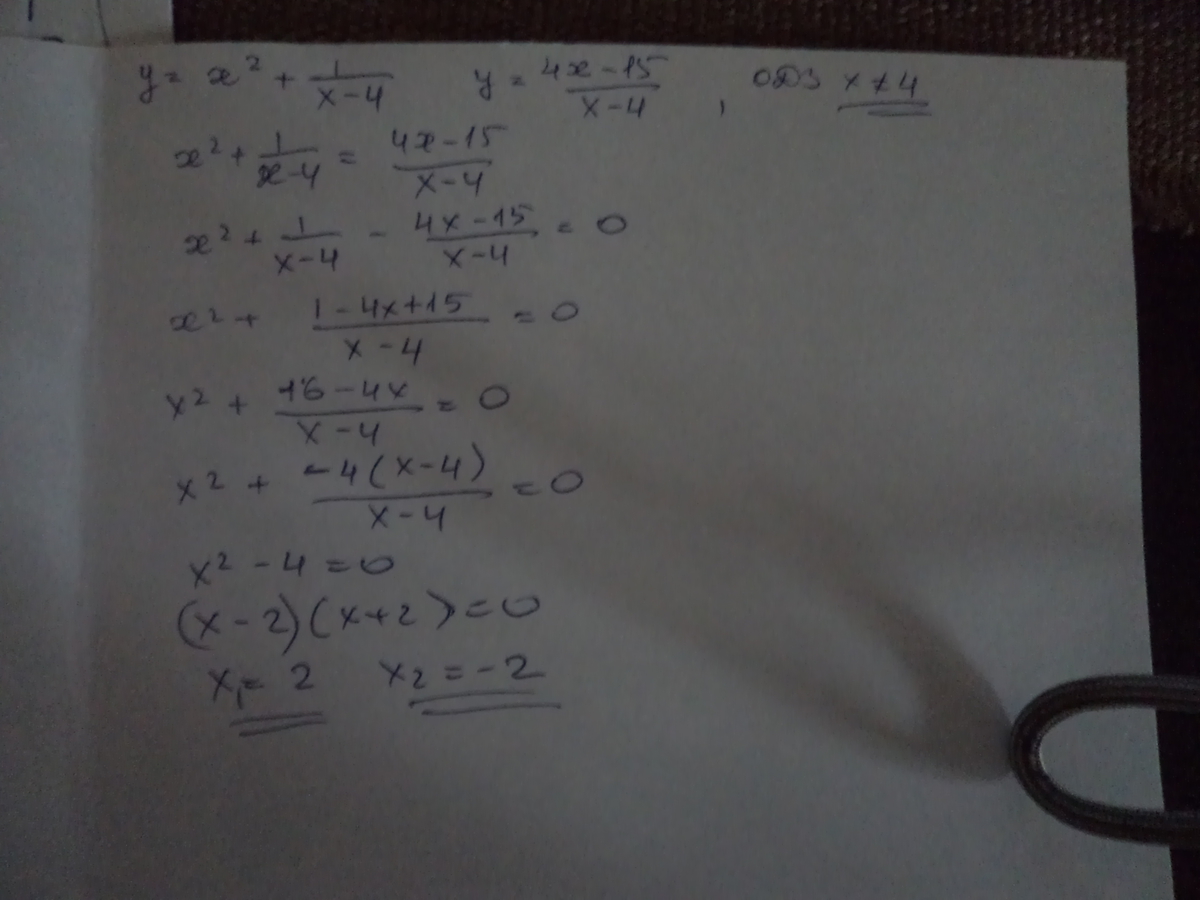

Автор ответа:
0
1.408a

Ответ: 3 и -0,6
1.410а

1.411a

Ответ: 3 и -0,6
1.410а
1.411a
Приложения:
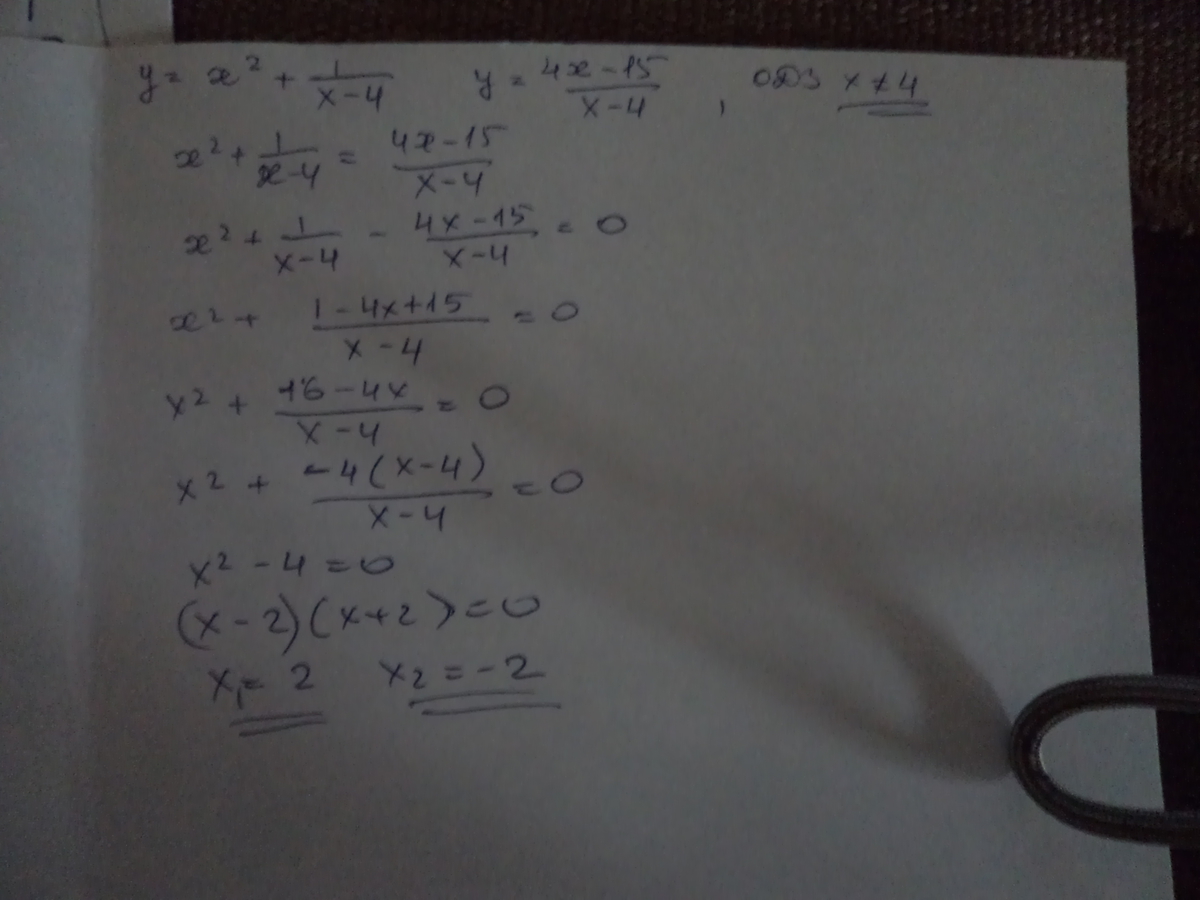

Похожие вопросы
Предмет: Русский язык,
автор: slavakuperman19
Предмет: Математика,
автор: zhalibaevv
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Алгебра,
автор: olyalavyagina
Предмет: История,
автор: Sonnq