Question

В тругольнике АВС угол С=90гр угол А= альфа, СВ=а .Точка Д не лежит в плоскости АВС , причем Дс перпендикулярно Са и Дс перпендикулярно СВ.Найдите расстояние от точки Д до плоскости АВС , если перпендикуляр ,проведеный из точки Д к прямой АВ образует влоскость АВС угол бэтта

Answer 1

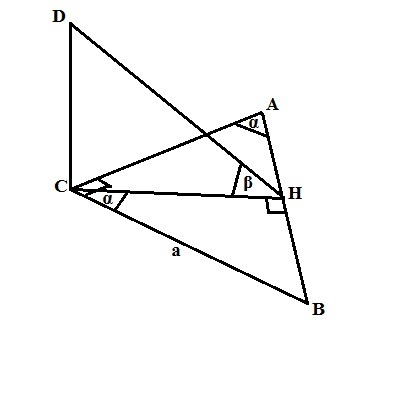
Перпендикуляр из точки D к прямой АВ и высота СН из прямого угла С прямоугольного треугольника АВС сойдутся в точке Н (так как по тереме о трех перпендикулярах наклонная DH перпендикулярна прямой АВ и значит ее проекция СН также перпендикулярна прямой АВ).
В прямоугольном треугольнике СНВ угол ВСН=углу А =α (доказывать не надо?). Тогда СН=АВ*Сosα или СН=a*Cosα.
В прямоугольном треугольнике DСН угол DСН=β (дано) и tgβ=DC/CH.
Тогда искомое расстояние DH=a*Coαs*tgβ.  Это ответ.